题目内容
已知数列{an}前n项和为Sn,首项为a1,且 ,an,Sn成等差数列.
,an,Sn成等差数列.
(1)求数列{an}的通项公式;
(2)数列{bn}满足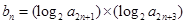 ,求证:
,求证: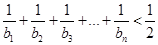 .
.
 ,an,Sn成等差数列.
,an,Sn成等差数列.(1)求数列{an}的通项公式;
(2)数列{bn}满足
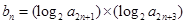 ,求证:
,求证: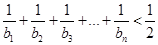 .
.(1) 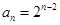 .(2)见解析.
.(2)见解析.
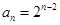 .(2)见解析.
.(2)见解析.试题分析:(1) 根据
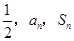 成等差数列,可得
成等差数列,可得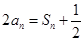 ,
, 当
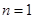 时,得到
时,得到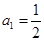 ,
, 当
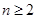 时,由
时,由 ,得到
,得到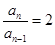 ,知数列
,知数列 是首项为
是首项为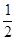 ,公比为2的等比数列.
,公比为2的等比数列.(2)
 由于
由于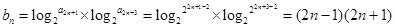
利用“裂项相消法”求和
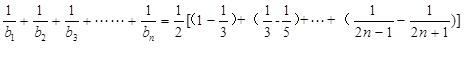
“放缩”即得.
试题解析:(1)

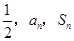 成等差数列,∴
成等差数列,∴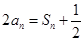 , 1分
, 1分当
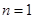 时,
时,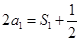 ,
,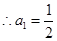 , 2分
, 2分当
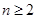 时,
时, ,
,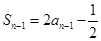 ,
,两式相减得:
 ,
,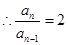 , 4分
, 4分所以数列
 是首项为
是首项为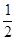 ,公比为2的等比数列,
,公比为2的等比数列,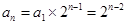 . 6分
. 6分(2)

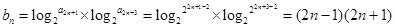
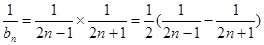 10分
10分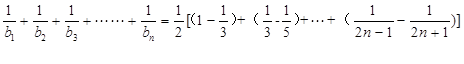
=
 . 12分
. 12分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
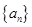 是首项和公比均为
是首项和公比均为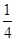 的等比数列,设
的等比数列,设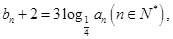 .
.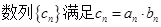
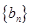 是等差数列;
是等差数列;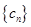 的前n项和
的前n项和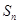 .
.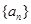 是公差不为0的等差数列,
是公差不为0的等差数列,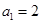 ,且
,且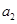 ,
,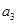 ,
,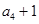 成等比数列.
成等比数列.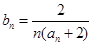 ,求数列
,求数列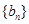 的前
的前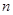 项和
项和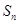 。
。 是递增的等差数列,
是递增的等差数列, ,
, 为其前
为其前 项和,若
项和,若 成等比数列,则
成等比数列,则 .
. 是点集A到点集B的一个映射,且对任意
是点集A到点集B的一个映射,且对任意 ,有
,有 .现对点集A中的点
.现对点集A中的点 ,
, ,均有
,均有 ,点
,点 为(0,2),则线段
为(0,2),则线段 的长度
的长度 .
.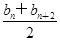 ≤bn+1(n∈N*);②bn≤M(n∈N*,M是与n无关的常数)的无穷数列{bn}叫“特界” 数列.
≤bn+1(n∈N*);②bn≤M(n∈N*,M是与n无关的常数)的无穷数列{bn}叫“特界” 数列. 中,
中, ,则数列
,则数列 _____________,设
_____________,设 ,则数列
,则数列 的前
的前 项和
项和 _____________.
_____________. 中,已知
中,已知 ,则
,则 ( )
( )


