题目内容

19．数列{an}是公差不为0的等差数列，且a1，a4，a5恰为某等比数列的前三项，那么该等比数列公比的值 为$\frac{1}{3}$．

分析 设数列{an}是公差d不为0的等差数列，等比数列的公比为q，由等比数列的中项的性质和等差数列的通项公式，化简整理可得首项与公差的关系，再由等比数列的定义，计算即可得到所求值．

解答 解：设数列{an}是公差d不为0的等差数列，等比数列的公比为q，
由a1，a4，a5恰为某等比数列的前三项，
即a1，a1+3d，a1+4d成等比数列，
可得${（{{a_1}+3d}）^2}={a_1}（{{a_1}+4d}）$，
解得${a_1}=-\frac{9}{2}d$，
即有q=$\frac{{a}_{4}}{{a}_{1}}$=$\frac{3d-\frac{9}{2}d}{-\frac{9}{2}d}$=$\frac{1}{3}$．
故答案为：$\frac{1}{3}$．

点评 本题考查等比数列的中项的性质，考查等差数列的通项公式的运用，化简整理的运算能力，属于基础题．

练习册系列答案
相关题目
9．已知等差数列{an}满足：a1+a5=4，则数列{2${\;}^{{a}_{n}}$}的前5项之积为1024（用数字作答）
10．在平面直角坐标系xOy中，过点M（0，1）的椭圆 Γ：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{6}}{3}$
（1）求椭圆 Γ的方程；
（2）已知直线l不过点M，与椭圆 Γ相交于P，Q两点，若△MPQ的外接圆是以PQ为直径，求证：直线l过定点，并求出该定点的坐标．
7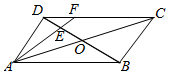．在平行四边形ABCD中，AC与BD交于点O，E是线段OD的中点，AE的延长线与CD相交于点F．若AB=2，$AD=\sqrt{2}$，∠BAD=45°，则$\overrightarrow{AF}•\overrightarrow{BE}$=（　　）
A．$\frac{1}{2}$B．1C．-$\frac{1}{2}$D．1
14．已知等比数列{an}的公比q＞1，且a1+a3=20，a2=8．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设${b_n}=\frac{n}{a_n}$，Sn是数列{bn}的前n项和，不等式${S_n}+\frac{n}{{{2^{n+1}}}}＞{（-1）^n}•a$对任意正整数n恒成立，求实数a的取值范围．
4．已知数列{an}是单调递减的等差数列，S6=S11，有以下四个结论：
（1）a9=0
（2）当n=8或n=9时，Sn取最大值
（3）存在正整数k使得Sk=0
（4）存在正整数m使得Sm=S2m
其中正确的是（1），（2），（3）．
11．在等比数列{an}中，已知${a_2}=\frac{1}{2}\;，\;\;{a_5}=4$，则此数列的公式比为2．
8．若复数z满足（-3+4i）$\overline{z}$=25i，其中i为虚数单位，则z=（　　）
A．4-3iB．4+3iC．-5+3iD．3+4i
9．已知定义在R上的函数y=f（x）满足条件f（x+$\frac{3}{2}$）=-f（x），且函数y=f（x-$\frac{3}{4}$）为奇函数，给出以下四个命题：
①函数f（x）是周期函数；
②函数f（x）的图象关于点（-$\frac{3}{4}$，0）对称；
③函数f（x）为R上的偶函数；
④函数f（x）为R上的单调函数；
其中真命题的序号为①②③（写出所有真命题的序号）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网