题目内容
已知在四棱锥 中,底面
中,底面 是矩形,且
是矩形,且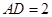 ,
,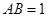 ,
,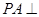 平面
平面 ,
,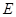 、
、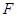 分别是线段
分别是线段 、
、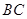 的中点.
的中点.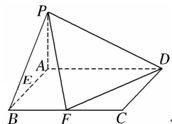
(1)证明: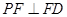 ;
;
(2)判断并说明 上是否存在点
上是否存在点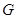 ,使得
,使得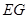 ∥平面
∥平面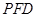 ;
;
(1)证明:见解析;(2)满足 的点
的点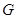 即为所求.
即为所求.
解析试题分析:(1)通过 ,证明得到
,证明得到 再利用
再利用 ,∴
,∴ ,推出“线线垂直”.
,推出“线线垂直”.
(2)注意运用已有的“平行关系”:过点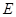 作
作 交
交 于点
于点 ,则
,则 ∥平面
∥平面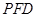 ,
,
且有 ,再过点
,再过点 作
作 ∥
∥ 交
交 于点
于点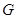 ,得到
,得到 ∥平面
∥平面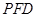 且
且 ,
,
根据平面 ∥平面推出
∥平面推出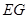 ∥平面
∥平面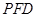 .
.
从而作出结论:满足 的点
的点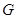 即为所求.
即为所求.
试题解析:证明:连接 ,则
,则 ,
, ,
,
又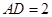 ,
,
∴ ,∴
,∴ 3分
3分
又 ,∴
,∴ ,又
,又 ,
,
∴ 6分
6分
(2)过点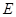 作
作 交
交 于点
于点 ,则
,则 ∥平面
∥平面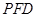 ,
,
且有 8分
8分
再过点 作
作 ∥
∥ 交
交 于点
于点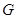 ,则
,则 ∥平面
∥平面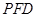 且
且 ,
,
∴ 平面 ∥平面
∥平面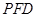 10分
10分
∴ 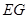 ∥平面
∥平面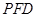 .
.
从而满足 的点
的点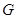 即为所求. 12分
即为所求. 12分
考点:平行关系,垂直关系.

练习册系列答案
相关题目
 中,底面
中,底面 是正方形,侧面
是正方形,侧面 底面
底面 ,
, 分别为
分别为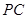 ,
, 中点,求证:
中点,求证: ∥平面
∥平面 ;
;
 ;
; ,求证:平面
,求证:平面 平面
平面 .
.
 中,底面
中,底面 是平行四边形,
是平行四边形, 平面
平面 ,
, ,
, .
.
 平面
平面 ;
; 平面
平面 .
.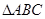 在平面
在平面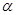 内,
内,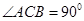 ,AB=2BC=2,P为平面
,AB=2BC=2,P为平面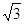 ,
,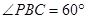
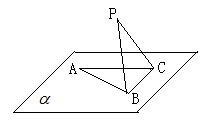
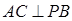
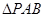 的面积取得最大值时,求直线PC与平面PAB所成角的正弦值
的面积取得最大值时,求直线PC与平面PAB所成角的正弦值 中,
中, ,
, ,
, ,点
,点 为
为 中点.将
中点.将 沿
沿 折起,使平面
折起,使平面
 平面
平面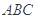 ,得到几何体
,得到几何体 ,如图2所示.
,如图2所示.
 上找一点
上找一点 ,使
,使 平面
平面 ;
; 到平面
到平面 的距离.
的距离.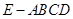 ,底面
,底面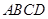 是矩形,平面
是矩形,平面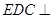 底面
底面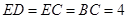 ,
,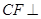 平面
平面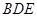 ,且点
,且点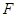 在
在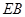 上.
上.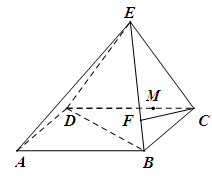
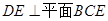 ;
;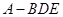 的体积;
的体积;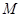 在线段
在线段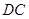 上,且满足
上,且满足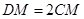 ,试在线段
,试在线段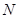 ,使得
,使得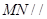 平面
平面 .
. ,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.
,平面ABCD⊥平面BCEG,BC=CD=CE=2AD=2BG=2.
 是AC的中点,已知
是AC的中点,已知 ,
, .
.
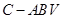 的体积.
的体积.