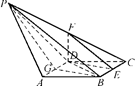
题目内容
如图1,在直角梯形 中,
中, ,
, ,
, ,点
,点 为
为 中点.将
中点.将 沿
沿 折起,使平面
折起,使平面
 平面
平面 ,得到几何体
,得到几何体 ,如图2所示.
,如图2所示.
(1)在 上找一点
上找一点 ,使
,使 平面
平面 ;
;
(2)求点 到平面
到平面 的距离.
的距离.
(1)详见解析;(2) .
.
解析试题分析:(1)取 的中点
的中点 ,连接
,连接 .利用三角形的中位线定理
.利用三角形的中位线定理 和线面平行的判定定理即可证明;
和线面平行的判定定理即可证明;
(2)利用等体积转化, ,
, 为等腰直角三角形,
为等腰直角三角形, ,
, 面
面 ,可证
,可证 ,得到
,得到 ,
, 为直角三角形,这样借助等体积转化求出点C到平面的距离,中档题型.
为直角三角形,这样借助等体积转化求出点C到平面的距离,中档题型.
试题解析:(1)取 的中点
的中点 ,连结
,连结 ,
, 2分
2分
在 中,
中,
 ,
, 分别为
分别为 ,
, 的中点
的中点
 为
为 的中位线
的中位线

 平面
平面
 平面
平面

 平面
平面 -6分
-6分
(2)设点 到平面ABD的距离为
到平面ABD的距离为

 平面
平面
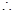

 而
而
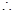
 即
即
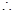

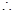 三棱锥
三棱锥 的高
的高 ,
,
 即
即



 12分
12分
考点:1.线面平行的判定;2.点到面的距离.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,PA=
,PA= ,∠ABC=120°,G为线段PC上的点.
,∠ABC=120°,G为线段PC上的点. 的值.
的值.
 平面ABCD,E,F分别为MA,DC的中点,求证:
平面ABCD,E,F分别为MA,DC的中点,求证:
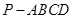 底面是菱形,
底面是菱形,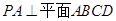 ,
,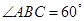 ,
,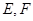 分别是
分别是 的中点.
的中点.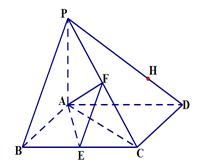
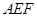 ⊥平面
⊥平面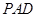 ;
;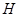 是
是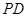 上的动点,
上的动点,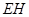 与平面
与平面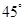 ,求二面角
,求二面角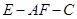 的正切值.
的正切值. 都为正方形,
都为正方形, ,F
,F 的中点,E为线段BC上的动点.
的中点,E为线段BC上的动点.
 平面AEF;
平面AEF;
 平面;
平面; ,写出
,写出 为何值时MF⊥平面AEF(结论不要求证明).
为何值时MF⊥平面AEF(结论不要求证明). 中,底面
中,底面 是矩形,且
是矩形,且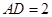 ,
,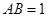 ,
,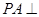 平面
平面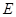 、
、 分别是线段
分别是线段 、
、 的中点.
的中点.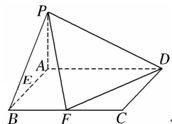
 ;
; 上是否存在点
上是否存在点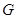 ,使得
,使得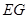 ∥平面
∥平面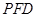 ;
; 于
于 (不同于点
(不同于点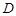 ),延长AE交BC于F,将△ABD沿BD折起,得到三棱锥
),延长AE交BC于F,将△ABD沿BD折起,得到三棱锥 ,如图2所示.
,如图2所示.
 //平面
//平面 ;
; ;
; 平面
平面 ,试判断直线
,试判断直线 与直线CD能否垂直?并说明理由.
与直线CD能否垂直?并说明理由. ,CE=EF=1.
,CE=EF=1.
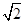 ,PB=2,E、F分别是BC、PC的中点.证明:AD⊥平面DEF.
,PB=2,E、F分别是BC、PC的中点.证明:AD⊥平面DEF.