题目内容
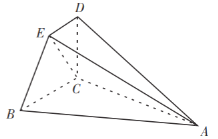
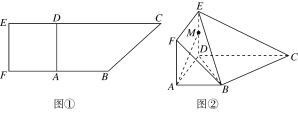
【题目】如图,![]() 是由两个全等的菱形
是由两个全等的菱形![]() 和
和![]() 组成的空间图形,
组成的空间图形,![]() ,∠BAF=∠ECD=60°.
,∠BAF=∠ECD=60°.
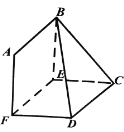
(1)求证:![]() ;
;
(2)如果二面角B-EF-D的平面角为60°,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)见解析;(2)![]()
【解析】
(1)取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,
,![]() .利用菱形的性质、等边三角形的性质分别证得
.利用菱形的性质、等边三角形的性质分别证得![]() ,
,![]() ,由此证得
,由此证得![]() 平面
平面![]() ,进而求得
,进而求得![]() ,根据空间角的概念,证得
,根据空间角的概念,证得![]() .
.
(2)根据(1)得到![]() 就是二面角
就是二面角![]() 的平面角,即
的平面角,即![]() ,由此求得
,由此求得![]() 的长.利用等体积法计算出
的长.利用等体积法计算出![]() 到平面
到平面![]() 的距离
的距离![]() ,根据线面角的正弦值的计算公式,计算出直线
,根据线面角的正弦值的计算公式,计算出直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
(1)取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,
,![]() .在菱形
.在菱形![]() 中,
中,
∵![]() ,∴
,∴![]() 是正三角形,∴
是正三角形,∴![]() ,
,
同理在菱形![]() ,可证
,可证![]() ,∴
,∴![]() 平面
平面![]() ,∴
,∴![]() ,
,
又∵![]() ,∴
,∴![]() .
.
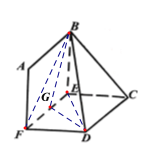
(2)由(1)知,![]() 就是二面角
就是二面角![]() 的平面角,即
的平面角,即![]() ,
,
又![]() ,所以
,所以![]() 是正三角形,故有
是正三角形,故有![]() ,
,
如图,取![]() 的中点
的中点![]() ,连接
,连接![]() ,则
,则![]() ,又由(1)得
,又由(1)得![]() ,
,
所以,![]() 平面
平面![]() ,且
,且![]() ,又
,又![]() ,在直角
,在直角![]() 中,
中,![]() ,
,
所以![]() ,设
,设![]() 到平面
到平面![]() 的距离为
的距离为![]() ,则
,则
![]() ,
,
![]() ,所以
,所以![]() ,
,
故直线![]() 与平面
与平面![]() 所成角正弦值为
所成角正弦值为![]() .
.

 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案【题目】新型冠状病毒肺炎疫情爆发以来,疫情防控牵挂着所有人的心. 某市积极响应上级部门的号召,通过沿街电子屏、微信公众号等各种渠道对此战“疫”进行了持续、深入的悬窗,帮助全体市民深入了解新冠状病毒,增强战胜疫情的信心. 为了检验大家对新冠状病毒及防控知识的了解程度,该市推出了相关的知识问卷,随机抽取了年龄在15~75岁之间的200人进行调查,并按年龄绘制频率分布直方图如图所示,把年龄落在区间![]() 和
和![]() 内的人分别称为“青少年人”和“中老年人”. 经统计“青少年人”和“中老年人”的人数比为19:21. 其中“青少年人”中有40人对防控的相关知识了解全面,“中老年人”中对防控的相关知识了解全面和不够全面的人数之比是2:1.
内的人分别称为“青少年人”和“中老年人”. 经统计“青少年人”和“中老年人”的人数比为19:21. 其中“青少年人”中有40人对防控的相关知识了解全面,“中老年人”中对防控的相关知识了解全面和不够全面的人数之比是2:1.
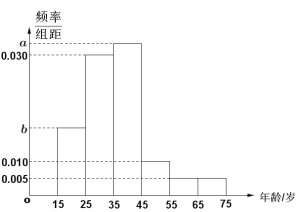
(1)求图中![]() 的值;
的值;
(2)现采取分层抽样在![]() 和
和![]() 中随机抽取8名市民,从8人中任选2人,求2人中至少有1人是“中老年人”的概率是多少?
中随机抽取8名市民,从8人中任选2人,求2人中至少有1人是“中老年人”的概率是多少?
(3)根据已知条件,完成下面的2×2列联表,并根据统计结果判断:能够有99.9%的把握认为“中老年人”比“青少年人”更加了解防控的相关知识?
了解全面 | 了解不全面 | 合计 | |
青少年人 | |||
中老年人 | |||
合计 |
附表及公式: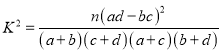 ,其中
,其中![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |