题目内容
13.在△ABC中,设内角A,B,C所对边分别为a,b,c,且sin(A-$\frac{π}{6}$)-cos(A+$\frac{5π}{3}$)=$\frac{\sqrt{2}}{2}$.(1)求角A的大小;
(2)若a=$\sqrt{5}$,sin2B+cos2C=1,求△ABC的面积.
分析 (1)利用诱导公式和两角和与差公式化简即可求解角A的大小.
(2)利用二倍角公式化简sin2B+cos2C=1,可得sin2B=2sin2C,利用正余弦定理即可求解b,c的大小.即可求解△ABC的面积.
解答 解:(1)sin(A-$\frac{π}{6}$)-cos(A+$\frac{5π}{3}$)=sin(A-$\frac{π}{6}$)-cos(2π-A$-\frac{5π}{3}$)=sin(A-$\frac{π}{6}$)-cos(A+$\frac{π}{3}$)
=$\frac{\sqrt{3}}{2}$sinA-$\frac{1}{2}$cosA-$\frac{1}{2}$cosA-$\frac{\sqrt{3}}{2}$sinA=$\frac{\sqrt{2}}{2}$
即cosA=$-\frac{\sqrt{2}}{2}$,
∵0<A<π,
∴A=$\frac{3π}{4}$.
(2)由sin2B+cos2C=1,可得sin2B=2sin2C,
由正弦定理,得b2=2c2,即$b=\sqrt{2}c$.a=$\sqrt{5}$,
cosA=$-\frac{\sqrt{2}}{2}$=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$,
解得:c=1,b=$\sqrt{2}$
∴△ABC的面积S=$\frac{1}{2}$bcsinA=$\frac{1}{2}$.
点评 本题考查了诱导公式和两角和与差公式化简和计算能力,同时考查了二倍角公式化简以及正余弦定理的运用.属于中档题.

练习册系列答案
相关题目
4.已知复数z=$\frac{(-1+i)(2+i)}{-i}$,则z在复平面内对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
1.执行如图的程序框图,如果输入的x∈[-1,3],输出的y∈[0,4],则输入的a的取值范围为( )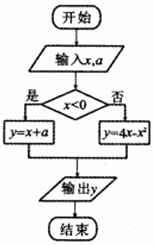

| A. | [-3,4] | B. | [1,4] | C. | [-3,0] | D. | [0,1] |
18.从某高中女学生中选取10名学生,根据其身高(cm)、体重(kg)数据,得到体重关于身高的回归方程$\widehat{y}$=0.85x-85,用来刻画回归效果的相关指数R2=0.6,则下列说法正确的是( )
| A. | 这些女学生的体重和身高具有非线性相关关系 | |
| B. | 这些女学生的体重差异有60%是由身高引起的 | |
| C. | 身高为170cm的学生体重一定为59.5kg | |
| D. | 这些女学生的身高每增加0.85cm,其体重约增加1kg |