题目内容
已知点 是双曲线
是双曲线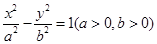 和圆
和圆 的一个交点,
的一个交点, 是双曲线的两个焦点,
是双曲线的两个焦点, ,则双曲线的离心率为
,则双曲线的离心率为
A. | B. | C.2 | D. |
A
解析试题分析:∵双曲线方程为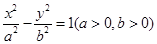 ,
,
∴双曲线的焦点坐标为F1(-c,0)、F2(c,0),其中c=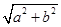 ,
,
∵圆方程为x2+y2=a2+b2,即x2+y2=c2
∴该半径等于c,且圆经过F1和F2.
∵点P是双曲线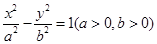 与圆x2+y2=a2+b2的交点,
与圆x2+y2=a2+b2的交点,
∴△PF1F2中,|OP|=c= |F1F2|,可得∠F1PF2=90°,∵∠PF2F1=2∠PF1F2,且∠PF2F1+∠PF1F2=90°,
|F1F2|,可得∠F1PF2=90°,∵∠PF2F1=2∠PF1F2,且∠PF2F1+∠PF1F2=90°,
∴∠PF1F2=30°,且∠PF2F1=60°,由此可得|PF1|= c,|PF2|=c,
c,|PF2|=c,
根据双曲线定义,可得2a=|PF1|-|PF2|=( -1)c,
-1)c,
∴双曲线的离心率e= ,故选A。
,故选A。
考点:本题主要考查双曲线的几何性质,圆的性质。
点评:中档题,在已知焦点三角形中的角度关系下求双曲线的离心率,往往需要探究三角形的特征,结合双曲线的定义,建立方程(组)加以解答。

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
若双曲线 与直线
与直线 无交点,则离心率
无交点,则离心率 的取值范围( )
的取值范围( )
A. | B. | C. | D. |
已知椭圆 上的一点
上的一点 到椭圆一个焦点的距离为
到椭圆一个焦点的距离为 ,则
,则 到另一焦点距离为
到另一焦点距离为
A. | B. | C. | D. |
过双曲线 的左焦点
的左焦点 作圆
作圆 的切线交双曲线右支于点
的切线交双曲线右支于点 ,切点为
,切点为 ,若
,若 ,则双曲线的离心率为
,则双曲线的离心率为
A. | B. | C. | D. |
 的左右焦点分别为
的左右焦点分别为 ,
, 为双曲线的离心率,P是双曲线右支上的点,
为双曲线的离心率,P是双曲线右支上的点, 的内切圆的圆心为I,过
的内切圆的圆心为I,过 作直线PI的垂线,垂足为B,则OB=
作直线PI的垂线,垂足为B,则OB=

 的离心率为
的离心率为 .双曲线
.双曲线 的渐近线与椭圆
的渐近线与椭圆 有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆
有四个交点,以这四个交点为顶点的四边形的面积为16,则椭圆
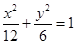


 与双曲线
与双曲线 相交于ABCD四点,若四边形ABCD是正方形,则双曲线的离心率的取值范围为( )
相交于ABCD四点,若四边形ABCD是正方形,则双曲线的离心率的取值范围为( )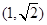



 的右顶点A作斜率为一1的直线,该直线与双曲线的两条渐近线的交点分别为B,C,若A,B,C三点的横坐标成等比数列,则双曲线的离心率为
的右顶点A作斜率为一1的直线,该直线与双曲线的两条渐近线的交点分别为B,C,若A,B,C三点的横坐标成等比数列,则双曲线的离心率为




 与抛物线
与抛物线 相交于
相交于 两点,F为抛物线的焦点,若
两点,F为抛物线的焦点,若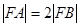 ,则k的值为( )。
,则k的值为( )。


