题目内容
5.若函数f(x)=lg(x2+ax-a-1)在区间[2,+∞)上单调递增,则实数a的取值范围是(-3,+∞).分析 令t=x2+ax-a-1,由外函数y=lgt为增函数,可知要使复合函数f(x)=lg(x2+ax-a-1)在区间[2,+∞)上单调递增,则$\left\{\begin{array}{l}{-\frac{a}{2}≤2}\\{{2}^{2}+2a-a-1>0}\end{array}\right.$,求解不等式组得答案.
解答 解:令t=x2+ax-a-1,
外函数y=lgt为增函数,要使复合函数f(x)=lg(x2+ax-a-1)在区间[2,+∞)上单调递增,
则$\left\{\begin{array}{l}{-\frac{a}{2}≤2}\\{{2}^{2}+2a-a-1>0}\end{array}\right.$,解得a>-3.
∴实数a的取值范围是:(-3,+∞).
故答案为:(-3,+∞).
点评 本题主要考查了复合函数的单调性以及单调区间的求法.对应复合函数的单调性,一要注意先确定函数的定义域,二要利用复合函数与内层函数和外层函数单调性之间的关系进行判断,判断的依据是“同增异减”,是中档题.

练习册系列答案
相关题目
17.正方体的内切球和外接球的表面积之比为( )
| A. | 1:2 | B. | 1:3 | C. | 1:4 | D. | 2:3 |
18.已知双曲线 C1:$\frac{x^2}{a^2}$-$\frac{y^2}{b^2}$=1( a>0,b>0),圆 C2:x2+y2-2ax+$\frac{3}{4}$a2=0,若双曲线C1 的一条渐近线与圆 C2 有两个不同的交点,则双曲线 C1 的离心率的范围是( )
| A. | (1,$\frac{{2\sqrt{3}}}{3}$) | B. | ($\frac{{2\sqrt{3}}}{3}$,+∞) | C. | (1,2) | D. | (2,+∞) |
2.某位股民购进某只股票,在接下来的交易时间内,他的这只股票先经历了5次涨停(每次上涨10%),又经历了5次跌停(每次下跌10%),则该股民这只股票的盈亏情况(不考虑其他费用)为( )
| A. | 略有盈利 | B. | 略有亏损 | ||
| C. | 没有盈利也没有亏损 | D. | 无法判断盈亏情况 |
17.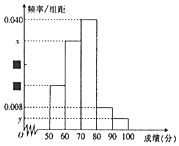 某中学举行了一次“环保知识竞赛”,全校学生参加了这次竞赛,为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计,请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:
某中学举行了一次“环保知识竞赛”,全校学生参加了这次竞赛,为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计,请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:
(1)写出a,b,x,y的值.
(2)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学到广场参加环保知识的志愿宣传活动.
①求所抽取的2名同学中至少有1名同学的成绩在[90,100]内的概率;
②求所抽取的2名同学来自同一组的概率.
 某中学举行了一次“环保知识竞赛”,全校学生参加了这次竞赛,为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计,请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:
某中学举行了一次“环保知识竞赛”,全校学生参加了这次竞赛,为了了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)作为样本进行统计,请根据下面尚未完成并有局部污损的频率分布表和频率分布直方图(如图所示)解决下列问题:| 组别 | 分组 | 频数 | 频率 |
| 第1组 | [50,60) | 8 | 0.16 |
| 第2组 | [60,70) | a |  |
| 第3组 | [70,80) | 20 | 0.40 |
| 第4组 | [80,90) |  | 0.08 |
| 第5组 | [90,100) | 2 | b |
| 合计 |  |  |
(2)在选取的样本中,从竞赛成绩是80分以上(含80分)的同学中随机抽取2名同学到广场参加环保知识的志愿宣传活动.
①求所抽取的2名同学中至少有1名同学的成绩在[90,100]内的概率;
②求所抽取的2名同学来自同一组的概率.
14.集合A={y|y=2x,x∈R},B={x∈Z|log6(x+2)<1},则A∩B=( )
| A. | {x|0<x<4} | B. | {1,2,3} | C. | {0,1,2,3} | D. | ∅ |