题目内容
若集合P={x|2x-a<0},Q={x|3x-b>0},a,b∈N,且P∩Q∩N={1},则满足条件的整数对(a,b)的个数为 .
【答案】分析:由集合P={x|x<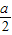 },Q={x|x>
},Q={x|x>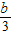 },得 P∩Q={x|
},得 P∩Q={x|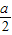 >x>
>x>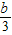 },由P∩Q∩N={1},a,b∈N,
},由P∩Q∩N={1},a,b∈N,
可得1<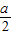 ≤2,1>
≤2,1>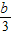 ≥0,故 a=3或4,b=0,1,2.
≥0,故 a=3或4,b=0,1,2.
解答:解:∵集合P={x|2x-a<0}={x|x<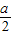 },Q={x|3x-b>0 }={x|x>
},Q={x|3x-b>0 }={x|x>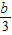 },a,b∈N,且P∩Q∩N={1},
},a,b∈N,且P∩Q∩N={1},
∴P∩Q={x|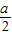 >x>
>x>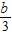 },
},
∴1<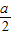 ≤2,1>
≤2,1>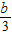 ≥0,∴2<a≤4,0≤b<3,∴a=3或4,b=0,1,2,
≥0,∴2<a≤4,0≤b<3,∴a=3或4,b=0,1,2,
故满足条件的整数对(a,b)的个数为6,
故答案为6.
点评:本题考查集合的表示方法,两个集合的交集的定义和求法,解不等式,求得a=3或4,b=0,1,2,是解题的关键.
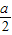 },Q={x|x>
},Q={x|x>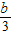 },得 P∩Q={x|
},得 P∩Q={x|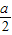 >x>
>x>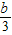 },由P∩Q∩N={1},a,b∈N,
},由P∩Q∩N={1},a,b∈N,可得1<
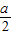 ≤2,1>
≤2,1>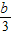 ≥0,故 a=3或4,b=0,1,2.
≥0,故 a=3或4,b=0,1,2.解答:解:∵集合P={x|2x-a<0}={x|x<
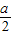 },Q={x|3x-b>0 }={x|x>
},Q={x|3x-b>0 }={x|x>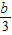 },a,b∈N,且P∩Q∩N={1},
},a,b∈N,且P∩Q∩N={1},∴P∩Q={x|
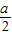 >x>
>x>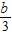 },
},∴1<
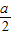 ≤2,1>
≤2,1>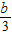 ≥0,∴2<a≤4,0≤b<3,∴a=3或4,b=0,1,2,
≥0,∴2<a≤4,0≤b<3,∴a=3或4,b=0,1,2,故满足条件的整数对(a,b)的个数为6,
故答案为6.
点评:本题考查集合的表示方法,两个集合的交集的定义和求法,解不等式,求得a=3或4,b=0,1,2,是解题的关键.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
若集合P={x|2x>
},Q={x||x-1|<2},则集合P与Q的关系为( )
| 1 |
| 2 |
| A、P∩Q={-1} |
| B、P∪Q=R |
| C、P⊆Q |
| D、P∩Q=Q |