若函数f(x)=$\left\{\begin{array}{l}{1-\sqrt{x}}\\{{2}^{x}}\end{array}\right.$.则f=$\frac{1}{2}$．题目和参考答案——青夏教育精英家教网—

题目内容

11．若函数f（x）=$\left\{\begin{array}{l}{1-\sqrt{x}（x≥0）}\\{{2}^{x}（x＜0）}\end{array}\right.$，则f（f（-2））=$\frac{1}{2}$．

分析由函数f（x）=$\left\{\begin{array}{l}{1-\sqrt{x}（x≥0）}\\{{2}^{x}（x＜0）}\end{array}\right.$，将x=-2代入计算可得答案．

解答解：∵函数f（x）=$\left\{\begin{array}{l}{1-\sqrt{x}（x≥0）}\\{{2}^{x}（x＜0）}\end{array}\right.$，
∴f（f（-2））=f（$\frac{1}{4}$）=$\frac{1}{2}$，
故答案为：$\frac{1}{2}$

点评本题考查的知识点是分段函数的应用，函数求值，难度不大，属于基础题．

练习册系列答案

2．计算：1og₂$\frac{1}{125}$•1og₃$\frac{1}{32}$•log₅$\frac{1}{3}$．

19．计算（log₂5+log₄125）（log₅4+log₂₅64）．

6．化简$\sqrt{（lg25）^{2}+lg25•lg16+（lg4）^{2}}$=2．

16．求下列各式中x的值：
（1）log_x27=$\frac{3}{2}$；
（2）4^x=5×3^x．

5．

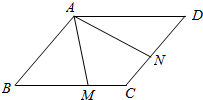如图，已知菱形ABCD的边长为2，∠BAD=120°，M，N分别为BC、CD上的点，$\overrightarrow{BM}$=λ$\overrightarrow{BC}$，$\overrightarrow{DN}$=μ$\overrightarrow{DC}$，λ，μ∈（0，1），记$\overrightarrow{AM}$=$\overrightarrow{a}$，$\overrightarrow{AN}$=$\overrightarrow{b}$．
（1）当λ=μ=$\frac{1}{2}$时，求|$\overrightarrow{a}$-$\overrightarrow{b}$|；
（2）若$\overrightarrow{a}$•$\overrightarrow{b}$=-2，求$\frac{1}{λ}$+$\frac{1}{μ}$的值．

2．已知函数f（x）=x²+2xf′（1），则曲线y=f（x）在x=1处的切线方程为2x+y+1=0．

3．若不等式kx²+2kx+2≥0对一切实数x恒成立，则实数k的取值范围为[0，2]．

试题分类