题目内容
15.联合国教科文组织规定:一个国家或地区60岁以上的人口占该国或该地区人口总数的10%以上(含10%),该国家或地区就进入了老龄化社会,结合统计数据发现,某地区人口数在一段时间内可近似表示为P(x)=$\frac{W}{1+0.35×(0.94)^{x-2010}}$(万),60岁以上的人口数可近似表示为L(x)=10×[1+k%•(x-2010)](万)(x为年份,W,k为常数),根据第六次全国人口普查公报,2010年该地区人口共计105万.(Ⅰ)求W的值,判断未来该地区的人口总数是否有可能突破142万,并说明理由;
(Ⅱ)已知该地区2013年恰好进入老龄化社会,请预测2040年该地区60岁以上人口数(精确到1万).
参考数据“0.942=0.88,0.943=0.83,139420=0.29,0.9430=0.16.
分析 (Ⅰ)利用2010年该地区人口共计105万求W的值,利用$\frac{142}{1+0.35×(0.94)^{x-2010}}$≥142,即可判断未来该地区的人口总数是否有可能突破142万;
(Ⅱ)利用该地区2013年恰好进入老龄化社会,求出k%≈$\frac{1}{30}$,即可预测2040年该地区60岁以上人口数.
解答 解:(Ⅰ)∵2010年该地区人口共计105万,
∴x=2010,P=$\frac{W}{1+0.35}$=105,
∴W≈142.
令$\frac{142}{1+0.35×(0.94)^{x-2010}}$≥142,
∴0.35×(0.94)x-2010≤0无解,
∴未来该地区的人口总数不可能突破142万;
(Ⅰ)∵该地区2013年恰好进入老龄化社会,
∴10×[1+k%•(2013-2010)]=10%×$\frac{142}{1+0.35×0.9{4}^{3}}$,
∴k%≈$\frac{1}{30}$,
∴x=2040,L(2040)≈10×[1+$\frac{1}{30}$•(2040-2010)]=20万
点评 本题考查利用数学知识解决实际问题,考查学生的计算能力,正确理解题意是关键.

练习册系列答案
相关题目
3.已知f(x-1)=2x,则f(3)=( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
10.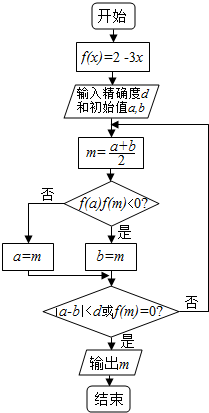 阅读如图所示的程序框图,若输出d=0.1,a=0,b=0.5,则输出的结果是( )
阅读如图所示的程序框图,若输出d=0.1,a=0,b=0.5,则输出的结果是( )
参考数据:
 阅读如图所示的程序框图,若输出d=0.1,a=0,b=0.5,则输出的结果是( )
阅读如图所示的程序框图,若输出d=0.1,a=0,b=0.5,则输出的结果是( )参考数据:
| x | f(x)=2x-3x |
| 0.25 | 0.44 |
| 0.375 | 0.17 |
| 0.4375 | 0.04 |
| 0.46875 | -0.02 |
| 0.5 | -0.08 |
| A. | 0.375 | B. | 0.4375 | C. | 0.46875 | D. | 0.5 |
7.设实数x,y满足$\left\{\begin{array}{l}{2x-y+1≤0}\\{y≤-x-k}\\{x≥0}\end{array}\right.$(k为常数),若目标函数z=3x-y的最大值为-$\frac{1}{3}$,则点(x,y)构成的平面区域Ω的面积为( )
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | 2 | D. | 4 |
19.如图所示,在正方体ABC-A1B1C1D1中,异面直线A1D与AB1所成角( )
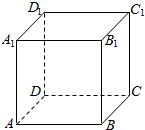

| A. | 30° | B. | 45° | C. | 60° | D. | 90° |