题目内容

17．函数f（x）=$\left\{\begin{array}{l}{2x+3，x≤0}\\{x+3，0＜x≤1}\\{-x+5，x＞1}\end{array}\right.$的最大值是（　　）
A．1B．2C．3D．4

分析 作出分段函数的图象，数形结合可得．

解答 解：作出分段函数f（x）=$\left\{\begin{array}{l}{2x+3，x≤0}\\{x+3，0＜x≤1}\\{-x+5，x＞1}\end{array}\right.$的图象（如图），
数形结合可得最大值为4，
故选：D．

点评 本题考查函分段函数图象，准确作图是解决问题的关键，属中档题．

练习册系列答案
相关题目
7．下列四个图形中，不是以x为自变量的函数的图象是（　　）
A．B．C．D．
8．已知在空间坐标系O-xyz中，点A（-1，2，3）关于平面xOz对称的点的坐标为（　　）
A．（1，2，3）B．（-1，-2，3）C．（-1，2，-3）D．（-1，-2，-3）
5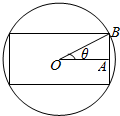．把截面半径为5的圆形木头锯成面积为y的矩形木料，如图，点O为圆心，OA⊥OB，设∠AOB=θ，把面积y表示为θ的表达式，则有（　　）
A．y=50cos2θB．y=25sinθC．y=25sin2θD．y=50sin2θ
12．已知函数$f（x）=\frac{1}{a}-\frac{1}{{{a^x}+1}}（{a＞1}）$．
（Ⅰ）证明：y=f（x）在R上是增函数；
（Ⅱ）当a=2时，方程f（x）=-2x+1的根在区间（k，k+1）（k∈Z）内，求k的值．
2．若函数f（x）=3x2-5x+a的一个零点在区间（-2，0）内，另一个零点在区间（1，3）内，则实数a的取值范围是（-12，0）．
9．已知函数f（x）=mx-m2-4，（m＞0，x∈R）．若a2+b2=8，则$\frac{f（b）}{f（a）}$的取值范围是（　　）
A．[$\sqrt{3}$-2，$\sqrt{3}$+2]B．[2-$\sqrt{3}$，2+$\sqrt{3}$]C．[0，2+$\sqrt{3}$]D．[0，2-$\sqrt{3}$]
6．对于函数f（x）=$\sqrt{x}$，当h无限趋近于0时，$\frac{\sqrt{3+h}-\sqrt{3}}{h}$无限趋近于$\frac{\sqrt{3}}{6}$，f′（3）=$\frac{\sqrt{3}}{6}$．
7．在$\sum_{k=1}^{n}（x+1）^{k}$展开式中含x2项系数与含x10项系数相等，则n取值为（　　）
A．12B．13C．14D．15

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网