题目内容
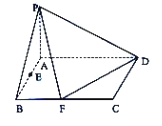
【题目】如图:在三棱锥![]() 中,
中,![]() ,
,![]() 是直角三角形,
是直角三角形,![]() ,
,
![]() ,点
,点![]() 分别为
分别为![]() 的中点.
的中点.

(1)求证:![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的大小;
所成角的大小;
(3)求二面角![]() 的正切值.
的正切值.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
试题以![]() 分别为
分别为![]() 轴建立空间直角坐标系,写出各点的坐标.(1)计算
轴建立空间直角坐标系,写出各点的坐标.(1)计算![]() ,可得两直线垂直;(2)计算直线
,可得两直线垂直;(2)计算直线![]() 的方向向量和平面
的方向向量和平面![]() 的法向量,可求得线面角的余弦值,用反三角函数表示出这个角的大小;(3)分别求出平面
的法向量,可求得线面角的余弦值,用反三角函数表示出这个角的大小;(3)分别求出平面![]() ,平面
,平面![]() 的法向量,利用法向量求两个平面所成角的余弦值,然后转化为正切值.
的法向量,利用法向量求两个平面所成角的余弦值,然后转化为正切值.
试题解析:
解法一(1)连接![]() 。在
。在![]() 中,
中,![]() .
.
![]() ,点
,点![]() 为
为![]() 的中点,
的中点,
∴![]() .
.
又![]() ,即
,即![]() 为
为![]() 在平面
在平面![]() 内的射影,∴
内的射影,∴![]() .
.
![]() 分别为
分别为![]() 的中点,
的中点,
∴![]() ,
,
∴![]() .
.
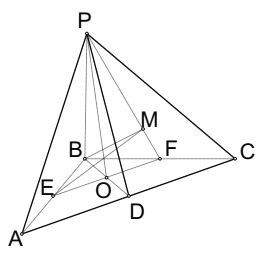
(2)![]() ,∴
,∴![]() .
.
连结![]() 交
交![]() 于点
于点![]() ,
,![]() ,∴
,∴![]() ,
,
∴![]() 为直线与
为直线与![]() 平面
平面![]() 所成的角,
所成的角,![]() .
.
![]() ,∴
,∴![]() ,又
,又![]() ,
,
∴![]() .
.![]() ,∴
,∴![]() ,
,
∴在![]() 中,
中,![]() ,∴
,∴![]() ,
,
即直线![]() 与平面
与平面![]() 所成角的大小为
所成角的大小为![]() .
.
(3)过点![]() 作
作![]() 于点
于点![]() ,连结
,连结![]() ,
,![]() ,
,
∴![]() ,即
,即![]() 为
为![]() 在平面
在平面![]() 内的射影,
内的射影,
![]() ,∴
,∴![]() 为二面角
为二面角![]() 的平面角.
的平面角.
∴![]() 中,
中,![]() ,
,
∴![]() ,即二面角
,即二面角![]() 的正切值为
的正切值为![]() .
.
解法二 建立空间直角坐标系![]() ,如图
,如图
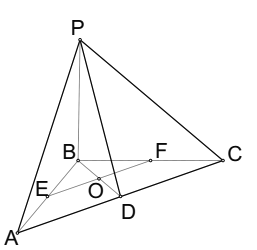
则![]() .
.
(1)∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)由已知可得![]() ,为平面的法向量,
,为平面的法向量,![]() ,
,
∴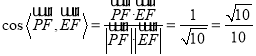 ,
,
∴直线![]() 与面
与面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
∴直线![]() 与面
与面![]() 所成角的为
所成角的为![]() .
.
(3)设平面![]() 的一个法向量为
的一个法向量为![]() ,
,
∴![]() ,
,
∴![]() ,令
,令![]() ,
,
∴![]() .
.
由已知可得,向量![]() 为平面
为平面![]() 的一个法向量,
的一个法向量,
∴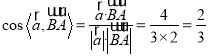 ,
,
∴![]() .
.
∴二面角![]() 的正切值为
的正切值为![]() .
.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
【题目】在测量一根新弹簧的劲度系数时,测得了如下的结果:
所挂重量( | 1 | 2 | 3 | 5 | 7 | 9 |
弹簧长度( | 11 | 12 | 12 | 13 | 14 | 16 |
(1)请在下图坐标系中画出上表所给数据的散点图;

(2)若弹簧长度与所挂物体重量之间的关系具有线性相关性,请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程![]() ;
;
(3)根据回归方程,求挂重量为![]() 的物体时弹簧的长度.所求得的长度是弹簧的实际长度吗?为什么?
的物体时弹簧的长度.所求得的长度是弹簧的实际长度吗?为什么?
注:本题中的计算结果保留小数点后两位.
(参考公式: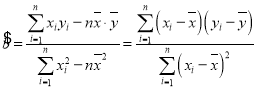 ,
,![]() )
)
(参考数据:![]() ,
,![]() )
)