题目内容
【题目】如图,在平面直角坐标系中,已知矩形![]() 的长为2,宽为1,
的长为2,宽为1, ![]() ,
, ![]() 边分别在
边分别在![]() 轴、
轴、![]() 轴的正半轴上,
轴的正半轴上, ![]() 点与坐标原点重合,将矩形折叠,使
点与坐标原点重合,将矩形折叠,使![]() 点落在线段
点落在线段![]() 上,设此点为
上,设此点为![]() .
.
(1)若折痕的斜率为-1,求折痕所在的直线的方程;
(2)若折痕所在直线的斜率为![]() ,(
,( ![]() 为常数),试用
为常数),试用![]() 表示点
表示点![]() 的坐标,并求折痕所在的直线的方程;
的坐标,并求折痕所在的直线的方程;
(3)当![]() 时,求折痕长的最大值.
时,求折痕长的最大值.

【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3) ![]() .
.
【解析】试题分析:(1)若折痕的斜率为![]() 时,由于
时,由于![]() 点落在线段
点落在线段![]() 上,可得折痕必过点
上,可得折痕必过点![]() ,即可得出;(2)当
,即可得出;(2)当![]() 时,此时
时,此时![]() 点与
点与![]() 点重合,折痕所在的直线方程
点重合,折痕所在的直线方程![]() ,当
,当![]() 时,将矩形折叠后
时,将矩形折叠后![]() 点落在线段
点落在线段![]() 上的点记为
上的点记为![]() ,可知
,可知![]() 与
与![]() 关于折痕所在的直线对称,有
关于折痕所在的直线对称,有![]() ,故
,故![]() 点坐标为
点坐标为![]() ,从而折痕所在的直线与
,从而折痕所在的直线与![]() 的交点坐标即线段
的交点坐标即线段![]() 的中点为
的中点为![]() ,即可得出;(3)当
,即可得出;(3)当![]() 时,折痕为2,当
时,折痕为2,当![]() 时,折痕所在直线交
时,折痕所在直线交![]() 于点
于点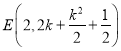 ,交
,交![]() 轴于
轴于 ,利用两点之间的距离公式、二次函数的单调性即可得出.
,利用两点之间的距离公式、二次函数的单调性即可得出.
试题解析:(1)∵折痕的斜率为![]() 时,
时, ![]() 点落在线段
点落在线段![]() 上
上
∴折痕必过点![]()
∴直线方程为![]()
(2)①当![]() 时,此时
时,此时![]() 点与
点与![]() 点重合,折痕所在的直线方程
点重合,折痕所在的直线方程![]() .
.
②当![]() 时,将矩形折叠后
时,将矩形折叠后![]() 点落在线段
点落在线段![]() 上的点记为
上的点记为![]() ,
, ![]()
则![]() 与
与![]() 关于折痕所在的直线对称,有
关于折痕所在的直线对称,有![]() ,即
,即![]() .
.
∴![]() 点坐标为
点坐标为![]()
从而折痕所在的直线与![]() 的交点坐标即线段
的交点坐标即线段![]() 的中点为
的中点为![]() ,折痕所在的直线方程
,折痕所在的直线方程![]() ,即
,即![]() .
.
综上所述,由①②得折痕所在的直线方程为: ![]() .
.
(3)当![]() 时,折痕长为2.
时,折痕长为2.
当![]() 时,折痕所在直线交
时,折痕所在直线交![]() 于点
于点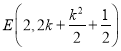 ,交
,交![]() 轴于
轴于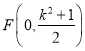 .
.
∵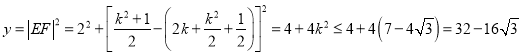 ,
,
∴折痕长的最大值为![]() .
.
∴综上所述,折痕长度的最大值为![]()

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目

