题目内容
2.设函数f(x)=$\left\{\begin{array}{l}{1,x>0}\\{0,x=0}\\{-1,x<0}\end{array}\right.$,g(x)=x2f(x-1),则函数g(x)的单调递减区间为[0,1).分析 根据f(x)的解析式便可求出f(x-1)的解析式,进而得出g(x)的解析式,根据解析式及二次函数、分段函数的单调性即可求出g(x)的单调递减区间.
解答 解:$f(x-1)=\left\{\begin{array}{l}{1}&{x>1}\\{0}&{x=1}\\{-1}&{x<1}\end{array}\right.$;
∴$g(x)=\left\{\begin{array}{l}{{x}^{2}}&{x>1}\\{0}&{x=1}\\{-{x}^{2}}&{x<1}\end{array}\right.$;
∴g(x)的单调递减区间为[0,1).
故答案为:[0,1).
点评 考查分段函数的定义,以及二次函数和分段函数的单调性.

练习册系列答案
相关题目
10.在一次招聘中,主考官要求应聘者从6道备选题中一次性随机抽取3道题,并独立完成所抽取的3道题.甲能正确完成其中的4道题,乙能正确完成每道题的概率为$\frac{2}{3}$,且每道题完成与否互不影响.
(1)记所抽取的3道题中,甲答对的题数为X,则X的分布列为
;
(2)记乙能答对的题数为Y,则Y的期望为E(Y)=2.
(1)记所抽取的3道题中,甲答对的题数为X,则X的分布列为
| X | 1 | 2 | 3 |
| P | 0.2 | 0.6 | 0.2 |
(2)记乙能答对的题数为Y,则Y的期望为E(Y)=2.
17.已知函数f(x)=$\left\{\begin{array}{l}{2^x},x≥0\\{log_2}(-x),x<0\end{array}$,则f(f(-2))=( )
| A. | -1 | B. | 2 | C. | 1 | D. | -2 |
14.已知函数$f(x)=\frac{1}{x}$,则f'(2)等于( )
| A. | 4 | B. | $\frac{1}{4}$ | C. | -4 | D. | $-\frac{1}{4}$ |
12.运行如图所示的程序框图,则输出结果为( )
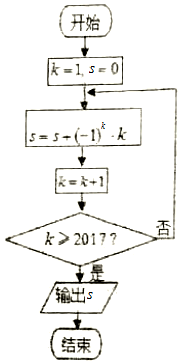

| A. | 2017 | B. | 2016 | C. | 1009 | D. | 1008 |