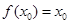题目内容
已知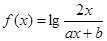 且
且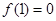 ,当
,当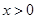 时,恒有
时,恒有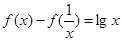
求 的解析式;
的解析式;
若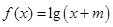 的解集为空集,求
的解集为空集,求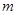 的范围。
的范围。
(1)  (2)
(2) 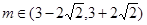
解析试题分析:解:当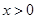 时,
时,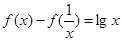 恒成立,得
恒成立,得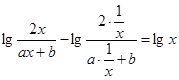 ,
,
∴ , 1分
, 1分
∴ax+b=a+bx对任意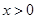 恒成立, 2分
恒成立, 2分
∴a=b 3分
又f(1)=0即 ,∴a=b=1, 4分
,∴a=b=1, 4分
∴ 5分
5分
方程 6分
6分
由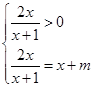 得
得 8分
8分
原方程的解为空集有两种情况
(1°)方程(1)无实根, 即
即 解得
解得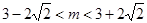 ···10分
···10分
(2°)方程(1)有实根,但两实根都在区间[-1,0]内,
令
则 得
得 无解 13分
无解 13分
综上:当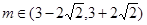 时,方程无解。 14分
时,方程无解。 14分
考点:二次不等式,函数解析式
点评:解决的关键是对于特殊值以及函数关系式恒成立来得到参数a,b的值,同时结合二次不等式为空集得到参数m的范围,属于中档题。

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
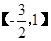 上的最大值和最小值.
上的最大值和最小值.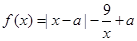 ,
,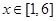 ,
,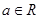 .
.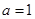 ,试判断并证明函数
,试判断并证明函数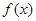 的单调性;
的单调性;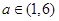 时,求函数
时,求函数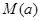 .
.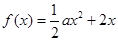 ,
, .
.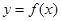 在
在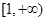 上是单调减函数,求
上是单调减函数,求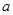 的取值范围;
的取值范围; ,使得方程
,使得方程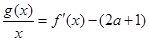 在区间
在区间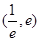 内有且只有两个不相等的实数根?若存在,请求出
内有且只有两个不相等的实数根?若存在,请求出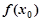 是函数
是函数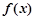 在点
在点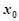 附近的某个局部范围内的最大(小)值,则称
附近的某个局部范围内的最大(小)值,则称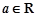 ,函数
,函数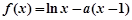 .
. ,求函数
,求函数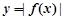 的极值点;
的极值点;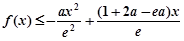 恒成立,求
恒成立,求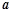 的取值范围.
的取值范围.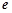 为自然对数的底数)
为自然对数的底数) ,函数
,函数
 的极小值;
的极小值; 在
在 上为单调增函数,求
上为单调增函数,求 的取值范围;
的取值范围; ,若在
,若在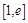 (
( 是自然对数的底数)上至少存在一个
是自然对数的底数)上至少存在一个 ,使得
,使得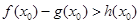 成立,求
成立,求 ,
,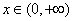 ,是否存在实数
,是否存在实数 ,使
,使 同时满足下列两个条件:(1)
同时满足下列两个条件:(1) 上是减函数,在
上是减函数,在 上是增函数;(2)
上是增函数;(2) ,若存在,求出
,若存在,求出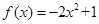 是偶函数,且在
是偶函数,且在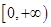 上是减少的。(13分)
上是减少的。(13分) ,总有
,总有 ;②
;② ;③若
;③若 ,则有
,则有 成立.
成立.  的值;(2) 函数
的值;(2) 函数 在区间[0,1]上是否同时适合①②③?并予以证明
在区间[0,1]上是否同时适合①②③?并予以证明 ,使得
,使得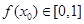 ,且
,且 ,求证:
,求证: