题目内容
(本小题满分12分)如图,设 为抛物线
为抛物线 的焦点,
的焦点, 是抛物线上一定点,其
是抛物线上一定点,其
坐为 ,
, 为线段
为线段 的垂直平分线上一点,且点
的垂直平分线上一点,且点 到抛物线的准线
到抛物线的准线 的距离为
的距离为 .
.
(Ⅰ)求抛物线的方程;(Ⅱ)过点P任作两条斜率均存在的直线PA、PB,分别与抛物线交于点A、B,如图示,若直线AB的斜率为定值 ,求证:直线PA、PB的倾斜角互补.
,求证:直线PA、PB的倾斜角互补.

(Ⅰ) (Ⅱ)证明过程见解析
(Ⅱ)证明过程见解析
【解析】
试题分析:对于第一问,根据点到准线的距离为 ,从而得出
,从而得出 的值,而得出结果,对于第二问,将倾斜角互补转化成斜率和为0,而直线的斜率用两点的斜率坐标公式,注意题的条件,斜率的关系,从而得出两点的坐标间的关系,已转化即可得结果.
的值,而得出结果,对于第二问,将倾斜角互补转化成斜率和为0,而直线的斜率用两点的斜率坐标公式,注意题的条件,斜率的关系,从而得出两点的坐标间的关系,已转化即可得结果.
试题解析:(Ⅰ)∵抛物线的方程为 ,∴直线
,∴直线 的方程为
的方程为 1分
1分
又∵点 在线段
在线段 的垂直平分线上,且
的垂直平分线上,且 为抛物线
为抛物线 的焦点,
的焦点,
∴点 的横坐标为
的横坐标为 . 2分
. 2分
又∵点 到抛物线的准线
到抛物线的准线 的距离为
的距离为 ,∴
,∴ ,即
,即 .
.
∴抛物线的方程为 . 5分
. 5分
(Ⅱ)设 ,则
,则 ,又因为点A、B均在抛物线
,又因为点A、B均在抛物线 上,所以有
上,所以有 ,所以
,所以 ,故由已知得
,故由已知得  (*) (7分)
(*) (7分)
又由已知易知 ,所以
,所以 从而有
从而有 (**) (8分)
(**) (8分)
又因为点A、B、P均在抛物线 上,所以有
上,所以有 把它们分别代入(**)式,并化简可得:
把它们分别代入(**)式,并化简可得:
 (10分)
(10分)
把(*)式代入,可得
故直线PA、PB的倾斜角互补。 (12分)
考点:抛物线的标准方程,直线与椭圆的关系,直线的斜率问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在一个2×2列联表中,由其数据计算得到K2的观测值k=13.097,则其两个变量间有关系的可能性为( )
A.99.9% B.95% C.90% D.0
附表:
| 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |

 B.
B.  C.
C.  D.
D. 
 中,
中, ,
, 点是内心,且
点是内心,且 ,则
,则 .
. :
: ,
, 的一边
的一边 为圆
为圆 长度的最大值是 .
长度的最大值是 .

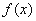 为奇函数,当
为奇函数,当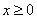 时,
时,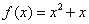 ,则
,则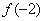 的值为 .
的值为 .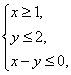 则
则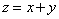 的最小值是___________.
的最小值是___________.