题目内容
17.已知集合M是满足下列性质的函数f(x)的全体:在定义域(0,+∞)内存在x0,使函数f(x0+1)≤f(x0)f(1)成立;
(1)请给出一个x0的值,使函数$f(x)=\frac{1}{x}∈M$;
(2)函数f(x)=x2-x-2是否是集合M中的元素?若是,请求出所有x0组成的集合;若不是,请说明理由;
(3)设函数$f(x)=\frac{a}{{{x^2}+2}}∈M$,求实数a的取值范围.
分析 (1)取值带入即可;
(2)根据函数f(x)的定义求解x0即可;
(3)利用函数的思想求解.
解答 解:(1)令x0=2,则$\frac{1}{3}≤\frac{1}{2}$,成立;
(2)假设函数f(x)=x2-x-2是集合M中的元素,则存在x0,使
f(x0+1)≤f(x0)f(1)成立,
即(x0+1)2-(x0+1)-2≤(${{x}_{0}}^{2}-{x}_{0}-2$)(-2),
解得:$\frac{1-\sqrt{73}}{6}≤{x}_{0}≤\frac{1+\sqrt{73}}{6}$,
故x0组成的集合是:{x0|$\frac{1-\sqrt{73}}{6}≤{x}_{0}≤\frac{1+\sqrt{73}}{6}$};
(3)∵函数f(x)=$\frac{a}{{x}^{2}+2}∈M$,
∴$\frac{a}{(x+1)^{2}+2}≤\frac{a}{{x}^{2}+2}•\frac{a}{3}$,
设g(x)=$\frac{3({x}^{2}+2)}{(x+1)^{2}+2}$=$\frac{3(1+\frac{2}{{x}^{2}})}{1+\frac{2}{x}+\frac{3}{{x}^{2}}}$,
∴0<g(x)<3,2
a=0时显然成立,
当a>0时,a>g(x),∴a>3;
a<0时,a<g(x),∴a<0;
综上,a≤0或a>3
点评 本题考查新定义及运用,考查运算和推理能力,考查函数的性质和应用,正确理解定义是迅速解题的关键,属于中档题

练习册系列答案
相关题目
7.函数f(x)=Asin(ωx+$\frac{π}{6}$)(A>0,ω>0)的图象与x轴的交点的横坐标构成一个公差为$\frac{π}{2}$的等差数列,要得到函数g(x)=Acosωx的图象,只需将f(x)的图象( )
| A. | 向左平移$\frac{π}{6}$个单位 | B. | 向右平移$\frac{π}{3}$个单位 | ||
| C. | 向左平移$\frac{2π}{3}$个单位 | D. | 向右平移$\frac{2π}{3}$个单位 |
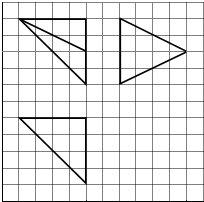 如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各个面中,直角三角形的个数是( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各个面中,直角三角形的个数是( ) 如图,在四面体PABC 中,面PAB,PBC,PAC两两垂直.
如图,在四面体PABC 中,面PAB,PBC,PAC两两垂直.