题目内容
11.求下列各角正弦、余弦、正切:(1)0;(2)π;(3)$\frac{3}{2}$π;(4)$\frac{2}{3}$π.
分析 由条件利用特殊角的三角函数的值,可得结论.
解答 解:(1)sin0=0,cos0=1,tan0=0.
(2)sinπ=0,cosπ=-1,tanπ=0.
(3)sin$\frac{3π}{2}$=-1,cos$\frac{3π}{2}$=0,tan$\frac{3π}{2}$不存在.
(4)sin$\frac{2π}{3}$=$\frac{\sqrt{3}}{2}$,cos$\frac{3π}{2}$=-$\frac{1}{2}$,tan$\frac{3π}{2}$=-$\sqrt{3}$.
点评 本题主要考查特殊角的三角函数的值,属于基础题.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
2.已知a+$\frac{1}{a}$=3,则a${\;}^{\frac{1}{2}}$+a${\;}^{-\frac{1}{2}}$等于( )
| A. | 2 | B. | $\sqrt{5}$ | C. | -$\sqrt{5}$ | D. | $±\sqrt{5}$ |
19.已知函数f(x)=2sin(π-x)•cosx-2sin2x+1,若f($\frac{{x}_{0}}{2}$)=$\frac{\sqrt{3}}{3}$,x0∈(-$\frac{π}{4}$,$\frac{π}{4}$),则cos2x0等于( )
| A. | $\frac{\sqrt{5}}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{2\sqrt{3}}{9}$ |
1.定义在R上的函数y=f(x)的值域为[0,1],则y=f(x+1)的值域为( )
| A. | [0,1] | B. | [1,2] | C. | [-1,0] | D. | 无法确定 |
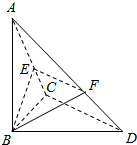 已知△ABC中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别为AC,AD上的动点,且AE:AC=AF:AD=k,k∈(0,1).
已知△ABC中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别为AC,AD上的动点,且AE:AC=AF:AD=k,k∈(0,1).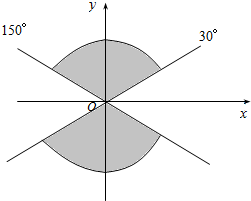 已知角α的终边在图中阴影部分所表示的范围内(不包括边界),则α的取值范围为{α|k•180°+30°<α<k•180°+150°,k∈Z}.
已知角α的终边在图中阴影部分所表示的范围内(不包括边界),则α的取值范围为{α|k•180°+30°<α<k•180°+150°,k∈Z}.