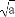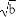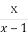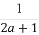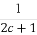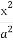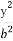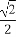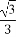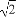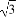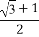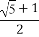题目内容
已知a,b,c,d均为正实数,且a+b+c+d=1,求证: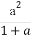
+
+
+
≥
.
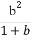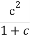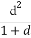见解析
【解析】证明：因为[(1+a)+(1+b)+(1+c)+(1+d)]·(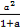
+
+
+
)≥(
·
+
·
+
·
+
·
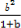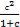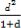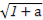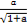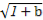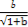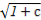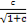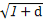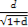)2=(a+b+c+d)2=1,
当且仅当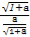
=
=
=
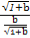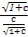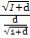即a=b=c=d=
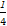时取等号.
又(1+a)+(1+b)+(1+c)+(1+d)
=4+(a+b+c+d)=5,
所以5(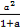++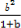+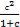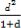)≥1.
所以+++≥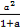
.
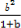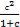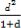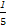练习册系列答案
相关题目
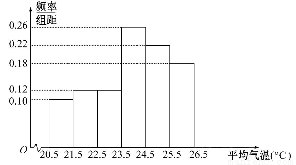
某高中共有学生2000名,各年级的男生、女生人数如下表.已知在全校学生中随机抽取1名,抽到二年级女生的概率是0.19,现用分层抽样的方法在全校抽取64名学生,则应在三年级抽取的学生人数为( )
| 一年级 | 二年级 | 三年级 |
女生 | 373 | x | y |
男生 | 377 | 370 | z |
(A)24 (B)18 (C)16 (D)12
