题目内容
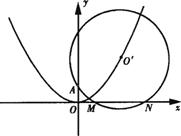
已知⊙O′过定点A(0,p)(p>0),圆心O′在抛物线x2=2py上运动,MN为圆O′在x轴上所截得的弦.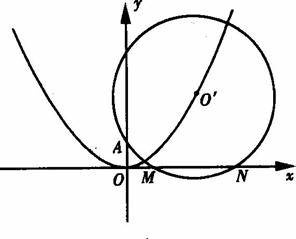
(Ⅰ)当O′点运动时,|MN|是否有变化?并证明你的结论;
(Ⅱ)当|OA|是|OM|与|ON|的等差中项时,试判断抛物线C的准线与圆O′的位置关系,并说明理由.
解:(Ⅰ)设O′(x0,y0),则![]() =2py0(y0≥0)则①O′的半径|O'A|=
=2py0(y0≥0)则①O′的半径|O'A|=![]()
①O′的方程为(x-x0)2+(y-y0)2=![]() +(y0-p)2令y=0,并把
+(y0-p)2令y=0,并把![]() =2py0代人得x2-2x0x+
=2py0代人得x2-2x0x+![]() -p2=0,
-p2=0,
解得x1=x0-p,x2=x0+p,∴|MN|+|x1-x2|=2p,
∴|MN|不变化,为定值2P.
(Ⅱ)不妨设M(x0-p,0),N(x0+p,0)由题2|OA|=|OM|+|ON|得2p=|x0-p|+|x0+p|
∴-p≤x0≤p
∵O′到抛物线准线y=![]() 的距离d=y0+
的距离d=y0+![]()
①O′的半径|O'A|=![]() =
=
∵r>d![]()
![]() +4p4>(
+4p4>(![]() +p2)2
+p2)2![]()
![]() <
<![]() p2:
p2:
又![]() ≤p2<
≤p2<![]() p2(p>0)
p2(p>0)
故r>d,即①O′与抛物线的准线总相交.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 已知⊙O′过定点A(0,p)(p>0),圆心O'在抛物线C:x2=2py上运动,MN为圆O′在x轴上所截得的弦.
已知⊙O′过定点A(0,p)(p>0),圆心O'在抛物线C:x2=2py上运动,MN为圆O′在x轴上所截得的弦.