题目内容
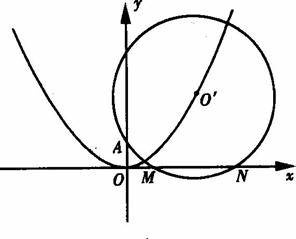
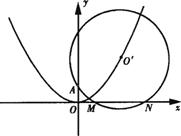
 已知⊙O′过定点A(0,p)(p>0),圆心O'在抛物线C:x2=2py上运动,MN为圆O′在x轴上所截得的弦.
已知⊙O′过定点A(0,p)(p>0),圆心O'在抛物线C:x2=2py上运动,MN为圆O′在x轴上所截得的弦.(1)当O′点运动时,|MN|是否有变化?并证明你的结论;
(2)当|OA|是|OM|与|ON|的等差中项且M,N在原点O的右侧时,试判断抛物线C的准线与圆O′是相交、相切还是相离,并说明理由.
分析:(1)先设出圆的方程,求出M,N两点的坐标表示出|MN|即可发现|MN|的取值是否变化.
(2)设M,N的中点为B,则|OM|+|ON|=2|OB|且O′B⊥MN,由|OA|=|OM|+|ON|,得|O′A|=
p.由此能够导出⊙Q与抛物线的准线总相交.
(2)设M,N的中点为B,则|OM|+|ON|=2|OB|且O′B⊥MN,由|OA|=|OM|+|ON|,得|O′A|=
| ||
| 2 |
解答:解:(1)设O′(x0,y0),则x02=2py0(y0≥0),则⊙O′的半径|O′A|=
(2分)
⊙O′的方程为(x-x0)2+(y-y0)2=x02+(y0-p)2
令y=0,并把x02=2py0代入得x2-2x0x+x02-p2=0,(3分)解得x1=x0-p,x2=x0+p,
∴|MN|=|x1-x2|=2p,(5分),∴|MN|不变化,为定值2p. (6分)
(2)设M,N的中点为B,则|OM|+|ON|=2|OB|且O′B⊥MN(8分)
又∵|OA|是|OM|与|ON|的等差中项,∴|OM|+|ON|=2|OA|,(9分)
可得B(p,0),O′(p,
)
∴|O′A|=
=
p(11分)
又∵点O′到抛物线C的准线的距离为
-(-
)=p<
p,∴圆O′与抛物线C的准线相交. (13分)
|
⊙O′的方程为(x-x0)2+(y-y0)2=x02+(y0-p)2
令y=0,并把x02=2py0代入得x2-2x0x+x02-p2=0,(3分)解得x1=x0-p,x2=x0+p,
∴|MN|=|x1-x2|=2p,(5分),∴|MN|不变化,为定值2p. (6分)
(2)设M,N的中点为B,则|OM|+|ON|=2|OB|且O′B⊥MN(8分)
又∵|OA|是|OM|与|ON|的等差中项,∴|OM|+|ON|=2|OA|,(9分)
可得B(p,0),O′(p,
| p |
| 2 |
∴|O′A|=
p2+(
|
| ||
| 2 |
又∵点O′到抛物线C的准线的距离为
| p |
| 2 |
| p |
| 2 |
| ||
| 2 |
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与圆锥曲线的相关知识,解题时要注意合理地进行等价转化.

练习册系列答案
相关题目