题目内容
已知向量 =(1,0),
=(1,0), =(x,1),若
=(x,1),若 •
• =2,则x=________;|
=2,则x=________;| +
+ |=________.
|=________.
2 
分析:根据向量数量的坐标运算公式,不难求得x=2,进而得到向量 +
+ 的坐标,最后用向量模的公式可求出|
的坐标,最后用向量模的公式可求出| +
+ |的值.
|的值.
解答:∵ =(1,0),
=(1,0), =(x,1),
=(x,1),
∴ •
• =1×x+0×1=2,即x=2
=1×x+0×1=2,即x=2
所以 =(2,1),可得
=(2,1),可得 +
+ =(3,1)
=(3,1)
∴| +
+ |=
|=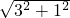 =
=
故答案为:2
点评:本题以向量的坐标运算为载体,考查了向量数量积的运算和向量模的公式等知识,属于基础题.

分析:根据向量数量的坐标运算公式,不难求得x=2,进而得到向量
 +
+ 的坐标,最后用向量模的公式可求出|
的坐标,最后用向量模的公式可求出| +
+ |的值.
|的值.解答:∵
 =(1,0),
=(1,0), =(x,1),
=(x,1),∴
 •
• =1×x+0×1=2,即x=2
=1×x+0×1=2,即x=2所以
 =(2,1),可得
=(2,1),可得 +
+ =(3,1)
=(3,1)∴|
 +
+ |=
|=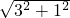 =
=
故答案为:2

点评:本题以向量的坐标运算为载体,考查了向量数量积的运算和向量模的公式等知识,属于基础题.

练习册系列答案
相关题目
已知向量
=(1,0),
=(
,
),则下列结论中正确的是( )
| a |
| b |
| 1 |
| 2 |
| 1 |
| 2 |
A、|
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、(
|