题目内容
7.下列命题中,真命题为( )| A. | ?x0∈R,e${\;}^{{x}_{0}}$≤0 | |
| B. | ?x∈R,2x>x2 | |
| C. | 已知a,b为实数,则a+b=0的充要条件是$\frac{a}{b}$=-1 | |
| D. | 已知a,b为实数,则a>1,b>1是ab>1的充分不必要条件. |
分析 对于A,B,C举例即可说明,对于D根据充分条件和必要条件的定义进行判断即可.
解答 解:对于A:因为ex>0恒成立,故A不正确,
对于B:当x=2时,不成立,故B不正确,
对于C:a=b=0时,则a+b=0,故C不正确,
对于D:由a>1,b>1⇒ab>1,当a=-2,b=-2时,满足ab>1,但不满足a>1,b>1,故a>1,b>1是ab>1的充分不必要条件,故D正确,
故选:D
点评 本题主要考查充分条件和必要条件和命题的真假的判断,根据不等式的关系是解决本题的关键.

练习册系列答案
相关题目
17.已知函数$f(x)=a{x^3}-2{x^2}+\frac{1}{2}x+\frac{1}{3}$,若f(x)至少存在一个大于0的零点x0,则实数a的取值范围是( )
| A. | $(-∞,-\frac{10}{3}]$ | B. | $[-\frac{10}{3},+∞)$ | C. | $(-∞,\frac{7}{6}]$ | D. | $[\frac{7}{6},+∞)$ |
18. 某校为了解校园安全教育系列活动的成效,对全校学生进行了一次安全意识测试,根据测试成绩评定“合格”、“不合格”两个等级,同时对相应等级进行量化:“合格”记5分,“不合格”记0分.现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如图所示:
某校为了解校园安全教育系列活动的成效,对全校学生进行了一次安全意识测试,根据测试成绩评定“合格”、“不合格”两个等级,同时对相应等级进行量化:“合格”记5分,“不合格”记0分.现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如图所示:
(Ⅰ)求a,b,c的值;
(Ⅱ)用分层抽样的方法,从评定等级为“合格”和“不合格”的学生中随机抽取10人进行座谈.现再从这10人这任选4人,记所选4人的量化总分为ξ,求ξ的分布列及数学期望E(ξ);
(Ⅲ)某评估机构以指标M(M=$\frac{E(ξ)}{D(ξ)}$,其中D(ξ)表示ξ的方差)来评估该校安全教育活动的成效.若M≥0.7,则认定教育活动是有效的;否则认定教育活动五校,应调整安全教育方案.在(Ⅱ)的条件下,判断该校是否应调整安全教育方案?
 某校为了解校园安全教育系列活动的成效,对全校学生进行了一次安全意识测试,根据测试成绩评定“合格”、“不合格”两个等级,同时对相应等级进行量化:“合格”记5分,“不合格”记0分.现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如图所示:
某校为了解校园安全教育系列活动的成效,对全校学生进行了一次安全意识测试,根据测试成绩评定“合格”、“不合格”两个等级,同时对相应等级进行量化:“合格”记5分,“不合格”记0分.现随机抽取部分学生的答卷,统计结果及对应的频率分布直方图如图所示:| 等级 | 不合格 | 合格 | ||
| 得分 | [20,40) | [40,60) | [60,80) | [80,100] |
| 频数 | 6 | a | 24 | b |
(Ⅱ)用分层抽样的方法,从评定等级为“合格”和“不合格”的学生中随机抽取10人进行座谈.现再从这10人这任选4人,记所选4人的量化总分为ξ,求ξ的分布列及数学期望E(ξ);
(Ⅲ)某评估机构以指标M(M=$\frac{E(ξ)}{D(ξ)}$,其中D(ξ)表示ξ的方差)来评估该校安全教育活动的成效.若M≥0.7,则认定教育活动是有效的;否则认定教育活动五校,应调整安全教育方案.在(Ⅱ)的条件下,判断该校是否应调整安全教育方案?
2.已知F1、F2为双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点,点P为双曲线C右支上一点,直线PF1与圆x2+y2=a2相切,且|PF2|=|F1F2|,则双曲线C的离心率为( )
| A. | $\frac{\sqrt{10}}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{5}{3}$ | D. | 2 |
6.已知函数$f(x)={e^{{x^2}+2x}}$,设$a=lg\frac{1}{5}\;\;,\;\;b={log_{\frac{1}{2}}}\frac{1}{3}\;\;,\;\;c={({\frac{1}{3}})^{0.5}}$,则有( )
| A. | f(a)<f(b)<f(c) | B. | f(a)<f(c)<f(b) | C. | f(b)<f(c)<f(a) | D. | f(b)<f(a)<f(c) |
7.设集合A={4,5,7,9},B={3,4,7,8,9},全集U=A∪B,则集合∁U(A∩B)的非空子集共有( )
| A. | 3个 | B. | 4个 | C. | 7个 | D. | 8个 |
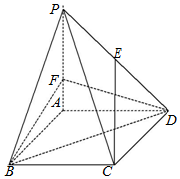 如图,在四棱锥P-ABCD中,底面ABCD是边长为 3 的菱形,∠ABC=60°,PA⊥平面ABCD,PA=3,F 是棱 PA上的一个动点,E为PD的中点.
如图,在四棱锥P-ABCD中,底面ABCD是边长为 3 的菱形,∠ABC=60°,PA⊥平面ABCD,PA=3,F 是棱 PA上的一个动点,E为PD的中点.