题目内容
20.已知a、b表示两条不同的直线,α,β表示两个不同的平面,则下列命题正确的是( )| A. | 若α∥β,a∥α,b∥β,则a∥b | B. | 若a?α,b?β,a∥b,则α∥β | ||
| C. | 若a⊥α,b⊥β,α⊥β,则a∥b | D. | 若a⊥α,b⊥β,a⊥b,则α⊥β |
分析 对四个选项分别进行判断,即可得出结论.
解答 解:A.若α∥β,a∥α,b∥β,则a、b平行、相交或异面,不正确;
B.若a?α,b?β,a∥b,则α,β平行或相交,不正确;
C.若a⊥α,b⊥β,且α⊥β,则由面面垂直的性质可知a⊥b,不正确;
D.因为a⊥α,a⊥b,所以b∥α 或b?α,因为b⊥β,所以α⊥β,正确.
故选:D.
点评 本题考空间中线面,面面,线线位置关系,解题的关键是有着较强的空间感知能力及对空间中线面,面面,线线位置关系的理解与掌握,此类题是训练空间想像能力的题,属于基本能力训练题.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
10.某学校组织高一高二两个年级的50名学生干部利用假期参加社会实践活动,活动内容是:①到社会福利院慰问孤寡老人;②到车站做义工,帮助需要帮助的旅客.各位同学根据各自的实际情况,选择了不同的活动项目,相关的数据如下表所示:
(1)用分层抽样的方法在到车站做义工的同学中随机抽取6名,求在高二年级的学生中应抽取几名?
(2)在(1)中抽取的6名同学中任取2名,求选到的同学为高二年级学生人数的数学期望;
(3)如果“到社会福利院慰问老人”与“到车站做义工”是两个分类变量,并且计算出随机变量K2=2.981,那么,你有多大把握认为选择到社会福利院慰问老人与到车站做义工是与年级有关系的?
| 到社会福利院慰问老人 | 到车站做义工 | 总计 | |
| 高一 | 11 | 16 | 27 |
| 高二 | 15 | 8 | 23 |
| 总计 | 26 | 24 | 50 |
(2)在(1)中抽取的6名同学中任取2名,求选到的同学为高二年级学生人数的数学期望;
(3)如果“到社会福利院慰问老人”与“到车站做义工”是两个分类变量,并且计算出随机变量K2=2.981,那么,你有多大把握认为选择到社会福利院慰问老人与到车站做义工是与年级有关系的?
| 参考数据 | P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
12.下列命题中的假命题是( )
| A. | ?x∈R,log2x=0 | B. | ?x∈R,x2>0 | C. | ?x∈R,tanx=0 | D. | ?x∈R,3x>0 |
9.已知集合A={x|0<log2x<2},B={y|y=3x+2,x∈R},则A∩B=( )
| A. | (1,4) | B. | (2,4) | C. | (1,2) | D. | (1,+∞) |
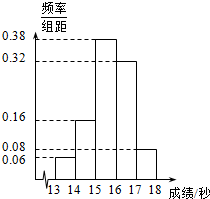 2015年08月22日至2015年08月30日在北京举行国际田联世界田径锦标赛,其中50名运动员在一次百米测试中,成绩全部介于13秒与18秒之间,来自牙买加的运动员博尔特取得最好的成绩.将测试结果按如下方式分成五组:第一组[13,14),第二组[14,15)…第五组[17,18],
2015年08月22日至2015年08月30日在北京举行国际田联世界田径锦标赛,其中50名运动员在一次百米测试中,成绩全部介于13秒与18秒之间,来自牙买加的运动员博尔特取得最好的成绩.将测试结果按如下方式分成五组:第一组[13,14),第二组[14,15)…第五组[17,18],