题目内容
5. 2015年08月22日至2015年08月30日在北京举行国际田联世界田径锦标赛,其中50名运动员在一次百米测试中,成绩全部介于13秒与18秒之间,来自牙买加的运动员博尔特取得最好的成绩.将测试结果按如下方式分成五组:第一组[13,14),第二组[14,15)…第五组[17,18],
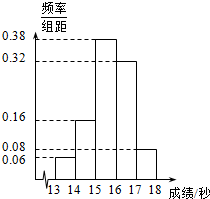
2015年08月22日至2015年08月30日在北京举行国际田联世界田径锦标赛,其中50名运动员在一次百米测试中,成绩全部介于13秒与18秒之间,来自牙买加的运动员博尔特取得最好的成绩.将测试结果按如下方式分成五组:第一组[13,14),第二组[14,15)…第五组[17,18],如图是按上述分组方法得到的频率分布直方图
(1)若成绩大于或等于14秒且小于16秒的认为良好,求50名运动员在这次百米测试中成绩良好的人数;
(2)设m,n表示50名运动员中某两名运动员的百米测试成绩,且已知m,n∈[13,14)∪[17,18],求事件“|m-n|>1”的概率.
分析 (1)根据频率分布直方图,利用频率、频数与样本容量的关系,求出对应的数值即可;
(2)根据频率分布直方图,求出对应的频数,利用列举法求出基本事件数,计算所求的概率即可.
解答 解:(1)由频率分布直方图知,
成绩在[14,16]秒内的人数为:
50×0.16+50×0.38=27人,
所以该批运动员成绩良好的人数为27人;
(2)由频率分布直方图知,
成绩在[13,14]秒的人数为50×0.06=3人,分别设为x,y,z;
成绩在[17,18]秒的人数为50×0.08=4人,分别设为A,B,C,D;
若m,n∈[13,14]时,有(x,y),(x,z),(y,z)共3种情况;
若m,n∈[17,18]时,有(A,B),(A,C),(A,D),(B,C),(B,D),(C,D)共6种情况;
若m,n分别在[13,14]和[17,18]内时,
| A | B | C | D | |
| x | ( x,A ) | ( x,B ) | ( x,C ) | ( x,D ) |
| y | ( y,A ) | ( y,B) | ( y,C ) | ( y,D ) |
| z | ( z,A ) | (z,B) | ( z,C ) | ( z,D ) |
所以,基本事件总数为21种,而事件“|m-n|>1”,
即m,n分别在[13,14]和[17,18]内时间,
所包含的基本事件种数为12,
所以P(“|m-n|>1”)=$\frac{12}{21}$=$\frac{4}{7}$.
点评 本题考查了频率分布直方图的应用问题,也考查了用列举法求古典概型的概率问题,是基础题目.

练习册系列答案
相关题目
15.已知函数f(x)=asin(πx+α)+bcos(πx+β),且f(4)=9,则f(2016)的值为( )
| A. | 9 | B. | -9 | C. | 3 | D. | -3 |
13.设f(x)=$\left\{\begin{array}{l}{x-3,x≥10}\\{f[f(x+5)],x<10}\end{array}\right.$,则f(6)的值为( )
| A. | 8 | B. | 7 | C. | 6 | D. | 5 |
20.已知a、b表示两条不同的直线,α,β表示两个不同的平面,则下列命题正确的是( )
| A. | 若α∥β,a∥α,b∥β,则a∥b | B. | 若a?α,b?β,a∥b,则α∥β | ||
| C. | 若a⊥α,b⊥β,α⊥β,则a∥b | D. | 若a⊥α,b⊥β,a⊥b,则α⊥β |
17.已知{an}各项为正的等比数列,其前n项和为Sn,若a3=4,S3=7,则公比q等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{2}$ | C. | 2 | D. | 3 |