题目内容
根据下列条件解三角形:
(1)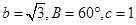 ;(2)
;(2)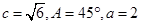 .
.
(1)
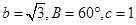 ;(2)
;(2)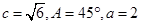 .
.(1) ,
, ,(2)
,(2)

 ,
, ,(2)
,(2)

试题分析:(1)解三角形就是要将三角形的角和边都求出来,一般利用正余弦定理进行求边和角.本题已知两边及一对角,可用正弦定理先求另一对角,即
 ,确定C角是否为钝角,需利用大边对大角,大角对应正弦值也大的规律,进行判断:
,确定C角是否为钝角,需利用大边对大角,大角对应正弦值也大的规律,进行判断: ∴
∴ ,∴
,∴ 为锐角, ∴
为锐角, ∴ ,
, .也可从余弦定理出发,先求
.也可从余弦定理出发,先求 ,即
,即 再利用正弦定理求角.(2)类似(1),不同点在于,
再利用正弦定理求角.(2)类似(1),不同点在于, ,所以要分情况讨论.
,所以要分情况讨论.试题解析:解:(1)
 ,∴
,∴ ,
, ,∴
,∴ ,∴
,∴ 为锐角,∴
为锐角,∴ ,∴
,∴ .
.(2)
 ,∴
,∴ ,∴
,∴ ,
,∴当
 ;
;∴当
 ;
;所以,

 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (其中ω>0,x∈R)的最小正周期为10π.
(其中ω>0,x∈R)的最小正周期为10π. ,
, ,
, ,求cos(α+β)的值.
,求cos(α+β)的值. ,则△ABC一定是 ( )
,则△ABC一定是 ( ) sinx+cosx,x∈[―
sinx+cosx,x∈[― ,
,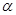 ,
,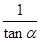 是关于x的方程x2-kx+k2-3=0的两个实根,且3π<
是关于x的方程x2-kx+k2-3=0的两个实根,且3π<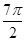 ,则cos
,则cos
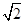
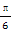 )-sin2x.
)-sin2x.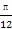 )的值.
)的值.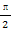 ],都有f(x)≤c,求实数c的取值范围.
],都有f(x)≤c,求实数c的取值范围. ,
, 的最小正周期为( )
的最小正周期为( )



 在函数
在函数 的图象上,则
的图象上,则 的值为 .
的值为 .