题目内容
设集合A={x|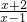
≤0}，B={x|x2-2x≤0}则（CRA）∩B=________．
[1，2]
分析：由A={x|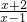≤0}，解分式不等式，即可求出集合A，求出集合A的补集，B={x|x2-2x≤0}解一元二次不等式，即可求出集合B，然后求它们的交集，
解答：A={x|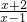≤0}={x|-2≤x＜1}，
∴CRA={x|x≥1或x＜-2}
B={x|x2-2x≤0}={x|0≤x≤2}，
∴（CRA）∩B=[1，2]．
故答案为：[1，2]．
点评：此题是个基础题．考查集合的交集和补集运算，以及分式不等式和一元二次不等式的解法．
分析：由A={x|
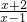≤0}，解分式不等式，即可求出集合A，求出集合A的补集，B={x|x2-2x≤0}解一元二次不等式，即可求出集合B，然后求它们的交集，解答：A={x|
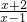≤0}={x|-2≤x＜1}，∴CRA={x|x≥1或x＜-2}
B={x|x2-2x≤0}={x|0≤x≤2}，
∴（CRA）∩B=[1，2]．
故答案为：[1，2]．
点评：此题是个基础题．考查集合的交集和补集运算，以及分式不等式和一元二次不等式的解法．
练习册系列答案
阅读快车系列答案
相关题目
设集合A={x|0≤x≤3}，B={x|x2-3x+2≤0，x∈Z}，则A∩B等于（ ）
| A、（-1，3） | B、[1，2] | C、{0，1，2} | D、{1，2} |