题目内容
(本小题满分12分)某电视台有一档综艺节目,其中有一个抢答环节,有甲、乙两位选手进行抢答,规则如下:若选手抢到答题权,答对得20分,答错或不答则送给对手10分.已知甲每次抢到答题权的概率为 ,且答对的概率为
,且答对的概率为 ,乙抢到答题权的概率为
,乙抢到答题权的概率为 ,且答对的概率为
,且答对的概率为 .
.
(1)在一轮抢答中,甲得到0分的概率;
(2)若比赛进行两轮,求甲得分的分布列及其期望.
(1) ;(2)分布列见解析,期望为
;(2)分布列见解析,期望为 .
.
【解析】
试题分析:(1)本题考查相互独立事件的概率问题,考查对于事件的掌握,“在一轮抢答中,甲得0分”这个事件包含“甲抢到答题权,但答错”和“乙抢到答题权,且答对”,因所求概率为 ;(2)由于比赛两轮,因此甲得到的分数可能有0,10,20,30,40五种可能,在求其概率时,要一一分析事件的各种可能,这里比较复杂的是
;(2)由于比赛两轮,因此甲得到的分数可能有0,10,20,30,40五种可能,在求其概率时,要一一分析事件的各种可能,这里比较复杂的是 这个事件,包含甲乙两人各抢到一次且都答对,两次都被甲抢到,但答对一次,答错一次,或者两次都被乙抢到,但都答错,由此可得P(X=20)=
这个事件,包含甲乙两人各抢到一次且都答对,两次都被甲抢到,但答对一次,答错一次,或者两次都被乙抢到,但都答错,由此可得P(X=20)= ,类似可求得其他的概率,最后利用期望公式可很快求得期望.
,类似可求得其他的概率,最后利用期望公式可很快求得期望.
试题解析:(1)P=
(2)设甲得分为X,X的可能取值为0,10,20,30,40
P(X=0)= P(X=10)=
P(X=10)=
P(X=20)= P(X=30)=
P(X=30)=
P(X=40)=
 .
.
考点:相互独立事件的概率,离散型随机变量的分布列与期望.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
 ,若
,若 在区间
在区间 上是增函数,则实数
上是增函数,则实数 的取值范围 .
的取值范围 .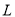 的参数方程为
的参数方程为 ,曲线
,曲线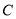 的参数方程为
的参数方程为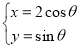 ,设直线
,设直线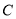 交于两点
交于两点
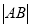 ;
;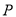 为曲线
为曲线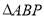 的面积取最大值时,求点
的面积取最大值时,求点
 的参数方程为
的参数方程为 ,曲线
,曲线 的参数方程为
的参数方程为 ,设直线
,设直线 交于两点
交于两点
 ;
; 为曲线
为曲线 的面积取最大值时,求点
的面积取最大值时,求点 的展开式中的常数项为 .
的展开式中的常数项为 .
 的中心位于点G
的中心位于点G ,A
,A ,动点P从A点出发沿
,动点P从A点出发沿 ,向量
,向量 在
在 方向的投影
方向的投影 的图像是( ).
的图像是( ).
 人,其年龄统计表如下:由于电脑故障,有两个数字在表格中不能显示出来,则下列说法正确的是( )
人,其年龄统计表如下:由于电脑故障,有两个数字在表格中不能显示出来,则下列说法正确的是( )
 ,众数是
,众数是
