题目内容
已知数列{an}满足a1=2，an=nan-1（n≥2），则a5=（ ）
| A、240 | B、120 |
| C、60 | D、30 |
考点：数列递推式
专题：点列、递归数列与数学归纳法
分析：由递推式an=nan-1（n≥2）可得
=n，利用“累乘求积”可得an=
×
×…×
×a1=2•n！即可得出．
| an |
| an-1 |
| an |
| an-1 |
| an-1 |
| an-2 |
| a2 |
| a1 |
解答：
解：∵an=nan-1（n≥2），
∴
=n，
∴an=
×
×…×
×a1=n×（n-1）×…×2×2=2•n!
∴a5=2×5!=240．
故选：A．
∴
| an |
| an-1 |
∴an=
| an |
| an-1 |
| an-1 |
| an-2 |
| a2 |
| a1 |
∴a5=2×5!=240．
故选：A．
点评：本题考查了数列递推式、“累乘求积”求数列的通项公式，属于中档题．
练习册系列答案
相关题目
化简
的结果是（ ）
| 1-sin260° |
| A、cos60° |
| B、-cos60° |
| C、±cos60° |
| D、±|cos60°| |
已知α=2，则点P（sinα，tanα）所在的象限是（ ）
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
从高三年级随机抽取100名学生，将他们的某次考试数学成绩绘制成频率分布直方图．由图中数据可知成绩在[130，140）内的学生人数为（ ）| A、20 | B、25 | C、30 | D、35 |
函数f（x）=log
（a-2x）-（2+x）有零点，则a的取值范围为（ ）
| 1 |
| 2 |
| A、（1，+∞） |
| B、[1，+∞） |
| C、（-∞，1] |
| D、（-∞，1） |
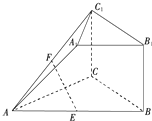如图所示的几何体中，四边形BB1C1C是矩形，BB1⊥平面ABC，CA=CB，A1B1∥AB，AB=2A1B1，E，F分别是AB，AC1的中点．
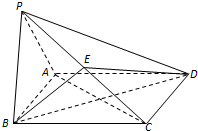如图，在四棱锥P-ABCD中，底面ABCD为矩形，平面PAB⊥平面ABCD，PA⊥PB，BP=BC，E为PC的中点．