题目内容
“ ”是“方程
”是“方程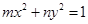 表示焦点在y轴上的椭圆”的( )
表示焦点在y轴上的椭圆”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
C
解析试题分析:题目中所给方程可以化成: ,应为
,应为 ,所以
,所以 ,所以表示焦点在
,所以表示焦点在 轴上的椭圆;若
轴上的椭圆;若 表示焦点在
表示焦点在 轴上的椭圆,需要
轴上的椭圆,需要 ,所以
,所以 ,所以“
,所以“ ”是“方程
”是“方程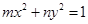 表示焦点在y轴上的椭圆”的充要条件.
表示焦点在y轴上的椭圆”的充要条件.
考点:本小题主要考查了椭圆的标准方程和充要条件的判断.
点评:首先应该把椭圆方程化成标准方程,然后注意两种标准方程的本质区别即可;判别充要条件时要分清哪个是条件,哪个是结论.

练习册系列答案
相关题目
命题:“若x2<1,则-1 ≤ x<1”的逆否命题是
| A.若x2≥1,则x<-1,或x≥1 | B.若-1≤x<1,则x2<1 |
| C.若x≤-1,或x>1,则x2≥1 | D.若x<-1,或x≥1,则x2≥1 |
命题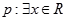 ,使
,使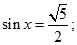 命题
命题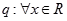 ,都有
,都有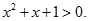
给出下列结论:① 命题“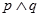 ”是真命题 ② 命题“
”是真命题 ② 命题“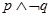 ”是假命题
”是假命题
③ 命题“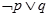 ”是真命题; ④ 命题“
”是真命题; ④ 命题“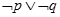 ”是假命题
”是假命题
其中正确的是
| A.② ④ | B.② ③ | C.③ ④ | D.① ② ③ |
设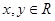 ,则“
,则“ 且
且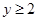 ”是“
”是“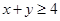 ”的 ( )
”的 ( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
命题“存在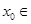 R,
R,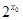
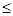 0”的否定是( )
0”的否定是( )
A.不存在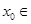 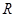 , ,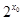 >0 >0 | B.存在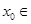 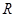 , , 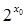 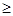 0 0 |
C.对任意的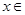 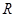 , , 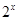 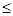 0 0 | D.对任意的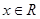 , ,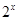 >0 >0 |
已知
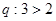 ,则下列判断中,错误的是( )
,则下列判断中,错误的是( )
| A.p或q为真,非q为假 | B.p或q为真,非p为假 |
| C.p且q为假,非p为真 | D.p且q为假,p或q为真 |
已知p:x2-x< 0,那么命题p的一个必要不充分条件是
| A.0 < x < 1 | B.-1< x < 1 |
C. < x < < x <  | D. < x < 2 < x < 2 |
 是
是
 的展开式中含有常数项的【 】
的展开式中含有常数项的【 】
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
 ,则一元二次方程
,则一元二次方程 有实根”的逆否命题是真命题
有实根”的逆否命题是真命题 0;则
0;则 p:?x∈R,均有x2+x+1
p:?x∈R,均有x2+x+1 0
0 为假,则命题
为假,则命题 为真,
为真, 为假
为假