题目内容
命题“存在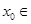 R,
R,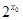
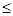 0”的否定是( )
0”的否定是( )
A.不存在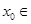 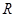 , ,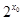 >0 >0 | B.存在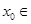 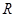 , , 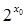 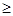 0 0 |
C.对任意的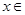 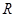 , , 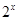 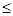 0 0 | D.对任意的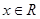 , ,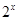 >0 >0 |
D
解析试题分析:根据命题“存在x0∈R,2x0≤0”是特称命题,其否定为全称命题,将“存在”改为“任意的”,将“≤”改为“>”即可得到答案。即
∵命题“存在x0∈R,2x0≤0”是特称命题
∴否定命题为:对任意的x∈R,2x>0.
故选D.
考点:本试题主要考查了全称命题与特称命题之间的转换,求解其否定的运用。
点评:解决该试题的关键是确定原命题是否为特称命题和全称命题,然后对于题目中的存在改为任意,结论改为否定即可。

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
设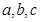
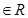 ,则“2b=a+c”是“a,b,c三个数成等差数列”的
,则“2b=a+c”是“a,b,c三个数成等差数列”的
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
设命题 在
在 内单调递增,命题
内单调递增,命题 ,则命题
,则命题 是命题
是命题 的: ( )
的: ( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
已知命题“ 或
或 ”为真,“非
”为真,“非 ”为假,则必有( )
”为假,则必有( )
A. 真 真 假 假 | B. 真 真 假 假 | C. 真 真 真 真 | D. 真, 真, 可真可假 可真可假 |
“ ”是“方程
”是“方程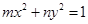 表示焦点在y轴上的椭圆”的( )
表示焦点在y轴上的椭圆”的( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知向量 ,则
,则 是
是 的( )
的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知命题 :
: ,
, .则
.则 是( )
是( )
A. , , | B. , , |
C. , , | D. , , |
设 , 那么“
, 那么“ ”是“
”是“ ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分又不必要条件 |
 有一根大于1,另一根小于1的充要条件是
有一根大于1,另一根小于1的充要条件是
 时,
时, 的最小值为1
的最小值为1 对于
对于 恒成立,则
恒成立,则
 的一个充分不必要条件是
的一个充分不必要条件是