题目内容
1.已知sin2α<0,cosα<0,则下列各式一定成立的是( )| A. | sinα<0 | B. | tanα>0 | C. | sinα+cosα>0 | D. | sinα-cosα>0 |
分析 根据题意,由sin2α<0,cosα<0分析可得cosα<0,则sinα>0,据此分析选项,综合即可得答案.
解答 解:根据题意,sin2α=2sinαcosα<0,即sinα、cosα符号相反,
又由cosα<0,则sinα>0,
据此分析选项:
对于A、sinα>0,故A错误,
对于B、tanα=$\frac{sinα}{cosα}$<0,故B错误,
对于C、cosα<0,则sinα>0,sinα+cosα>0不一定正确;C错误,
对于D、cosα<0,则sinα>0,必有sinα-cosα>0,D正确;
故选:D.
点评 本题考查三角函数的恒等变形,关键是掌握二倍角的正弦公式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12.今有苹果m个(m∈N+),分给10个同学,每个同学都分到苹果,恰好全部分完.第一个人分得全部苹果的一半还多一个,第二个人分得第一个人余下苹果的一半还多一个,以此类推,后一个人分得前一个人余下的苹果的一半还多一个,则苹果个数m为( )
| A. | 2046 | B. | 1024 | C. | 2017 | D. | 2018 |
9.已知集合M={x|x2≤9},N={x|x≤1},则M∩N=( )
| A. | [-3,1] | B. | [1,3] | C. | [-3,3] | D. | (-∞,1] |
6.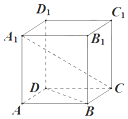 如图,四棱柱ABCD-A1B1C1D1的底面是菱形且D1D⊥平面ABCD,则A1C与BD所成的角是( )
如图,四棱柱ABCD-A1B1C1D1的底面是菱形且D1D⊥平面ABCD,则A1C与BD所成的角是( )
 如图,四棱柱ABCD-A1B1C1D1的底面是菱形且D1D⊥平面ABCD,则A1C与BD所成的角是( )
如图,四棱柱ABCD-A1B1C1D1的底面是菱形且D1D⊥平面ABCD,则A1C与BD所成的角是( )| A. | 90° | B. | 60° | C. | 45° | D. | 30° |
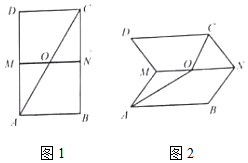 如图1,2,已知ABCD是矩形,M,N分别为边AD,BC的中点,MN与AC交于点O,沿MN将矩形MNCD折起,设AB=2,BC=4,二面角B-MN-C的大小为θ.
如图1,2,已知ABCD是矩形,M,N分别为边AD,BC的中点,MN与AC交于点O,沿MN将矩形MNCD折起,设AB=2,BC=4,二面角B-MN-C的大小为θ.