题目内容

15．湖心有四座小岛，其中任何三座都不在一条直线上．拟在它们之间修建3座桥，以便从其中任何一座小岛出发皆可通过这三座桥到达其它小岛．则不同的修桥方案有（　　）
A．4种B．16种C．20种D．24种

分析 本题是一个分类计数问题，．要把四个小岛连接起来，共有6个位置可以建设桥梁，要建三座有C63种结果，其中有4种情况是围成三角形，不合题意，减去不合题意的，得到结果．

解答 解：由题意知本题是一个分类计数问题，
要把四个小岛连接起来，共有6个位置可以建设桥梁，要建三座有C63=20种结果，
其中有4种情况是围成三角形，不合题意，不则不同的修桥方案有20-4=16种．
故选B．

点评 本题考查分类计数原理，是一个基础题，这种题目在解题时注意要减去不合题意的情况，即用三座桥连接起三个小岛．

练习册系列答案
相关题目
5．已知函数f（x）=$\frac{a+lnx}{x}$在x=1处取得极值．
（1）求a的值，并讨论函数f（x）的单调性；
（2）当x∈[1，+∞）时，f（x）≥$\frac{m}{1+x}$恒成立，求实数m的取值范围．
6．若f（x）是幂函数，且满足$\frac{f（9）}{f（3）}$=2，则f（$\frac{1}{9}$）=$\frac{1}{4}$．
3．设定义域为R的奇函数$f（x）=\frac{1}{{{2^x}+a}}-\frac{1}{2}$（a为实数）．
（Ⅰ）求a的值；
（Ⅱ）判断f（x）的单调性（不必证明），并求出f（x）的值域；
（Ⅲ）若对任意的x∈[1，4]，不等式f（k-$\frac{2}{x}$）+f（2-x）＞0恒成立，求实数k的取值范围．
10．某工厂生产A、B、C三种不同型号的产品，产品数量之比依次为2：3：5，现用分层抽样方法抽出一个容量为n的样本，样本中B种型号产品比A种型号产品多8件．那么此样本的容量n=（　　）
A．80B．120C．160D．60
20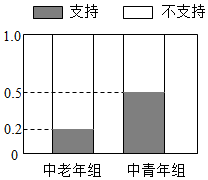．国家实施二孩放开政策后，为了了解人们对此政策持支持态度是否与年龄有关，计生部门将已婚且育有一孩的居民分成中老年组（45岁以上，含45岁）和中青年组（45岁以下，不含45岁）两个组别，每组各随机调查了50人，对各组中持支持态度和不支持态度的人所占的频率绘制成等高条形图，如图所示：
支持不支持合计
中老年组104050
中青年组252550
合 计3565100
（1）根据以上信息完成2×2列联表；
（2）是否有99%以上的把握认为人们对此政策持支持态度与年龄有关？
P（K2≥k0）0.0500.0100.001
k03.8416.63510.828
附：${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$．
7．执行如图所示的程序，若输出的结果为2，则输入的x的值为（　　）
A．0或-1B．0或2C．-1或2D．-1或0或2
4．已知集合M={y|y=-x2+4}，N={x|y=log2x}，则M∩N=（　　）
A．[4，+∞）B．（-∞，4]C．（0，4）D．（0，4]
5．如图1，四边形ABCD为直角梯形，AD∥BC，AD⊥AB，AD=1，BC=2，E为CD上一点，F为BE的中点，且DE=1，EC=2，现将梯形沿BE折叠（如图2），使平面BCE⊥ABED．
（1）求证：平面ACE⊥平面BCE；
（2）能否在边AB上找到一点P（端点除外）使平面ACE与平面PCF所成角的余弦值为$\frac{\sqrt{6}}{3}$？若存在，试确定点P的位置，若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网