Question

【题目】已知直线和圆.有以下几个结论：

①直线的倾斜角不是钝角；

②直线必过第一、三、四象限；

③直线能将圆分割成弧长的比值为的两段圆弧；

④直线与圆相交的最大弦长为；

其中正确的是______________.（写出所有正确说法的番号）

Answer 1

【答案】①④

【解析】

在①中，直线的方程可化为，从而直线的斜率的取值范围是，由此得到直线的倾斜角不是钝角；

在②中，直线的方程为，其中，得当时，直线不过第一、三、四象限；

在③中，圆心到直线的距离，从而直线与圆相交，圆截直线所得的弦所对的圆心角小于，从而得出直线不能将圆分割成弧长的比为的两段圆弧；

在④中，由圆心到直线的距离，得直线与圆相交的最大弦长为.

解：在①中，直线的方程可化为，

于是直线的斜率为，

，，

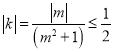当且仅当时，等号成立，

，直线的斜率的取值范围是，

直线的倾斜角不是钝角，故①正确.

在②中，直线的方程为，其中，

当时，直线不过第一、三、四象限，故②错误.

在③中，直线的方程为，其中，

圆的方程可化为，

圆的圆心为，半径，

于是圆心到直线的距离为，

由，得，即，

若直线与圆相交，则圆截直线所得的弦所对的圆心角小于，

故直线不能将圆分割成弧长的比为的两段圆弧，故③错误.

在④中，由③知圆心到直线的距离，

直线与圆相交的最大弦长为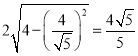，故④正确.

故答案为：①④.