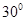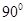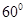题目内容
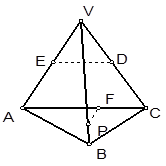
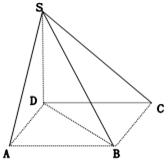
边长为4的正四面体P-ABC中,E为PA的中点,则平面EBC与平面ABC所成锐二面角的余弦值为______.
取BC的中点F,连接EF,AF,
∵四面体P-ABC为正四面体,
∴EF⊥BC,AF⊥BC,
∴∠EFA为平面EBC与平面ABC所成锐二面角,
∵边长为4,E为PA的中点,
∴EA=2,AF=2
,EF⊥AP,
∴EF=
=2
,
∴cos∠EFA=
=
=
,
故答案为:
.

∵四面体P-ABC为正四面体,
∴EF⊥BC,AF⊥BC,
∴∠EFA为平面EBC与平面ABC所成锐二面角,
∵边长为4,E为PA的中点,
∴EA=2,AF=2
| 3 |
∴EF=
(2
|
| 2 |
∴cos∠EFA=
| EF |
| AF |
2
| ||
2
|
| ||
| 3 |
故答案为:
| ||
| 3 |


练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目

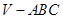 中,
中,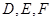 分别是
分别是 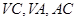 的中点,
的中点,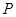 为
为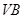 上任意一点,则直线
上任意一点,则直线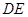 与
与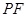 所成的角的大小是 ( )
所成的角的大小是 ( )