题目内容
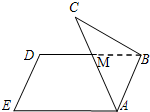
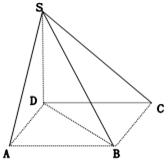
如图,多面体ABCDS中,面ABCD为矩形,SD⊥AD,SD⊥AB,且AB=2AD,SD=
AD,
(1)求证:平面SDB⊥平面ABCD;
(2)求二面角A-SB-D的大小.
| 3 |
(1)求证:平面SDB⊥平面ABCD;
(2)求二面角A-SB-D的大小.

(1)∵SD⊥AD,SD⊥AB,AD∩AB=A
∴SD⊥平面ABCD,
又∵SD⊆平面SBD,
∴平面SDB⊥平面ABCD.…(5分)
(2)由题可知DS、DA、DC两两互相垂直.
如图建立空间直角坐标系D-xyz
设AD=a,则S(
a,0,0),A(0,a,0),B(0,a,2a),C(0,0,2a),…(6分)
∵
=(
a,0,0),
=(0,a,2a),…(7分)
设面SBD的一个法向量为
=(x,y,-1)
则
,即
解得
=(0,2,-1)…(8分)
又∵
=(0,0,2a),
=(-
a,a,0),
设面SAB的一个法向量为
=(1,y,z),
则
,即
解出
=(1,
,0),…(10分)
cos<
,
>=
=
故所求的二面角为arccos
…(12分)
∴SD⊥平面ABCD,
又∵SD⊆平面SBD,
∴平面SDB⊥平面ABCD.…(5分)
(2)由题可知DS、DA、DC两两互相垂直.
如图建立空间直角坐标系D-xyz
设AD=a,则S(
| 3 |
∵
| DS |
| 3 |
| DB |
设面SBD的一个法向量为
| n |
则
|
|
解得
| n |
又∵
| AB |
| SA |
| 3 |
设面SAB的一个法向量为
| m |
则
|
|
解出
| m |
| 3 |
cos<
| m |
| n |
| ||||
|
|
| ||
| 15 |
故所求的二面角为arccos
| ||
| 15 |

练习册系列答案
相关题目