题目内容
已知函数：f（x）=lg[sin（2x+
）-
]
（1）求函数定义域
（2）求函数的值域
（3）若y=f（x+φ）是偶函数，求φ的集合．
| π |
| 3 |
| 1 |
| 2 |
（1）求函数定义域
（2）求函数的值域
（3）若y=f（x+φ）是偶函数，求φ的集合．
考点：复合三角函数的单调性,对数函数的图像与性质,对数函数图象与性质的综合应用
专题：计算题,函数的性质及应用,三角函数的图像与性质
分析：（1）要使函数有意义，则需sin（2x+
）-
＞0，由正弦函数的图象和性质，即可得到定义域；
（2）运用正弦函数的值域，结合对数函数的单调性，即可得到值域；
（3）运用余弦函数的奇偶性，即有2φ+
=kπ+
，k∈Z，解方程即可得到所求集合．
| π |
| 3 |
| 1 |
| 2 |
（2）运用正弦函数的值域，结合对数函数的单调性，即可得到值域；
（3）运用余弦函数的奇偶性，即有2φ+
| π |
| 3 |
| π |
| 2 |
解答：
解：（1）要使函数有意义，则需
sin（2x+
）-
＞0，即sin（2x+
）＞
，
即2kπ+
＜2x+
＜2kπ+
，k∈Z，
解得kπ-
＜x＜kπ+
，k∈Z，
则定义域为（kπ-
，kπ+
），k∈Z；
（2）由0＜sin（2x+
）-
≤
，
即有lg[sin（2x+
）-
]≤lg
=-lg2，
则值域为（-∞，-lg2]；
（3）y=f（x+φ）是偶函数，
即f（x+φ）=lg[sin（2x+2φ+
）-
]为偶函数，
则2φ+
=kπ+
，k∈Z，
解得φ=
+
，k∈Z．
则所求集合为{φ|φ=
+
，k∈Z}．
sin（2x+
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| 1 |
| 2 |
即2kπ+
| π |
| 6 |
| π |
| 3 |
| 5π |
| 6 |
解得kπ-
| π |
| 12 |
| π |
| 4 |
则定义域为（kπ-
| π |
| 12 |
| π |
| 4 |
（2）由0＜sin（2x+
| π |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
即有lg[sin（2x+
| π |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
则值域为（-∞，-lg2]；
（3）y=f（x+φ）是偶函数，
即f（x+φ）=lg[sin（2x+2φ+
| π |
| 3 |
| 1 |
| 2 |
则2φ+
| π |
| 3 |
| π |
| 2 |
解得φ=
| kπ |
| 2 |
| π |
| 12 |
则所求集合为{φ|φ=
| kπ |
| 2 |
| π |
| 12 |
点评：本题考查函数的定义域和值域以及奇偶性的运用，考查三角函数的图象和性质，考查对数函数的性质，考查运算能力，属于基础题．
练习册系列答案
相关题目
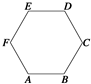
如图，在正六边形ABCDEF中，
+
+
等于（ ）
| BA |
| CD |
| FB |
| A、0 | ||
B、
| ||
C、
| ||
D、
|
直线x=tan60°的倾斜角是（ ）
| A、90° | B、60° |
| C、30° | D、没有倾斜角 |