Question

判断命题“若a≥0，则x²＋x－a＝0有实根”的逆否命题的真假．

Answer 1

解　法一　写出逆否命题，再判断其真假．

原命题：若a≥0，则x²＋x－a＝0有实根．

逆否命题：若x²＋x－a＝0无实根，则a＜0.

判断如下：

∵x²＋x－a＝0无实根，

∴Δ＝1＋4a＜0，∴a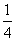＜－＜0，

∴“若x²＋x－a＝0无实根，则a＜0”为真命题．

法二　利用原命题与逆否命题同真同假(即等价关系)判断

∵a≥0，∴4a≥0，∴4a＋1＞0，

∴方程x²＋x－a＝0的判别式Δ＝4a＋1＞0，

∴方程x²＋x－a＝0有实根，

故原命题“若a≥0，则x²＋x－a＝0有实根”为真．

又∵原命题与其逆否命题等价，

∴“若a≥0，则x²＋x－a＝0有实根”的逆否命题为真命题．

法三　利用充要条件与集合关系判断．

命题p：a≥0，q：x²＋x－a＝0有实根，

∴p：A＝{a∈R|a≥0}，

q：B＝{a∈R|方程x²＋x－a＝0有实根}＝.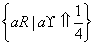

即A⊆B，∴“若p，则q”为真，

∴“若p，则q”的逆否命题“若綈q，则綈p”为真．

∴“若a≥0，则x²＋x－a＝0有实根”的逆否命题为真．