题目内容
已知数列 的前
的前 项和为
项和为 ,
, (
( ).
).
(1)证明数列 是等比数列,求出数列
是等比数列,求出数列 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列 的前
的前 项和
项和 ;
;
解:(Ⅰ)因为 ,所以
,所以 ,
,
则 ,所以
,所以 ,
,
 ,
,
所以数列 是等比数列,
是等比数列,
 ,
, ,
,
所以 .
.
(Ⅱ) ,
,
 ,
,
令 ,①
,①
 ,②
,②
①-②得, ,
,
 ,
,
所以 . …………10分
. …………10分
(Ⅲ)设存在 ,且
,且 ,使得
,使得 成等差数列,则
成等差数列,则 ,
,
即 , …………12分
, …………12分
即 ,
, ,因为
,因为 为偶数,
为偶数, 为奇数,
为奇数,
所以 不成立,故不存在满足条件的三项.
不成立,故不存在满足条件的三项.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,点F是PB的中点,点E在边BC上移动.
,点F是PB的中点,点E在边BC上移动.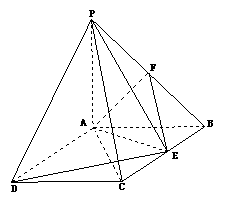
 中,已知
中,已知 上,则
上,则 的通项公式为_____________
的通项公式为_____________ 中,
中, =24,则前13项之和等于 ( )
=24,则前13项之和等于 ( ) }的前n 项和为
}的前n 项和为 ,已知
,已知 ,
, ,
, 成等差数列
成等差数列 ; (2)求
; (2)求 -
- =3,求
=3,求