题目内容
【题目】在平面直角坐标系xOy中,双曲线![]() :
:![]() 经过点
经过点![]() ,其中一条近线的方程为
,其中一条近线的方程为![]() ,椭圆
,椭圆![]() :
:![]() 与双曲线
与双曲线![]() 有相同的焦点
有相同的焦点![]() 椭圆
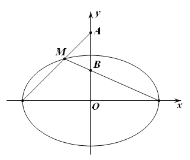
椭圆![]() 的左焦点,左顶点和上顶点分别为F,A,B,且点F到直线AB的距离为
的左焦点,左顶点和上顶点分别为F,A,B,且点F到直线AB的距离为![]() .
.
![]() 求双曲线
求双曲线![]() 的方程;
的方程;
![]() 求椭圆
求椭圆![]() 的方程.
的方程.
【答案】(1)![]() (2)
(2)![]()
【解析】
![]() 由双曲线经过点
由双曲线经过点![]() ,可得m;再由渐近线方程可得m,n的方程,求得n,即可得到所求双曲线的方程;
,可得m;再由渐近线方程可得m,n的方程,求得n,即可得到所求双曲线的方程;
![]() 由椭圆的a,b,c的关系式,求得F,A,B的坐标,可得直线AB的方程,由点到直线的距离公式,可得a,b的关系式,解方程可得a,b,进而得到所求椭圆方程.
由椭圆的a,b,c的关系式,求得F,A,B的坐标,可得直线AB的方程,由点到直线的距离公式,可得a,b的关系式,解方程可得a,b,进而得到所求椭圆方程.
解:![]() 双曲线
双曲线![]() :
:![]() 经过点
经过点![]() ,
,
可得![]() ,
,
其中一条近线的方程为![]() ,可得
,可得![]() ,
,
解得![]() ,
,![]() ,
,
即有双曲线![]() 的方程为
的方程为![]() ;
;
![]() 椭圆
椭圆![]() :
:![]() 与双曲线
与双曲线![]() 有相同的焦点,
有相同的焦点,
可得![]() ,
,![]()
椭圆![]() 的左焦点,左顶点和上顶点分别为
的左焦点,左顶点和上顶点分别为![]() ,
,![]() ,
,![]() ,
,
由点F到直线AB:![]() 的距离为
的距离为![]() ,可得
,可得
![]() ,化为
,化为![]() ,
,![]()
由![]() 解得
解得![]() ,
,![]() ,
,
则椭圆![]() 的方程为
的方程为![]() .
.

练习册系列答案
 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目