题目内容
18．已知a＞2，b＞2，则a+b与ab的大小关系是（ ）| A． | a+b＞ab | B． | a+b＜ab | C． | a+b≥ab | D． | a+b≤ab |
分析 a＞2，b＞2，可得（a-2）（b-2）＞0，化简即可得出．
解答 解：∵a＞2，b＞2，
∴（a-2）（b-2）＞0，化为：ab-（a+b）＞a+b-4＞0，
∴ab＞a+b．
故选：B．
点评 本题考查了作差法比较数的大小、不等式的性质，考查了推理能力与计算能力，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
8．在数列-1，0，$\frac{1}{9}$，$\frac{1}{8}$，…中，0.08是它的第几项（ ）
| A． | 10 | B． | 9 | C． | 11 | D． | 8 |
9．
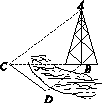如图，测量河对岸的塔高AB时，可以选与塔底B在同一水平面内的两个观测点C与D，测得∠BCD=15°，∠BDC=135°，CD=30m，并在点C处测得塔顶A的仰角为30°，则塔高AB
为（ ）
如图，测量河对岸的塔高AB时，可以选与塔底B在同一水平面内的两个观测点C与D，测得∠BCD=15°，∠BDC=135°，CD=30m，并在点C处测得塔顶A的仰角为30°，则塔高AB为（ ）
| A． | 10$\sqrt{2}$ m | B． | 10$\sqrt{3}$ m | C． | 15$\sqrt{6}$ m | D． | 10$\sqrt{6}$ m |
6．（文）曲线y=x3-3x在点（2，2）的切线斜率是（ ）
| A． | -1 | B． | 6 | C． | -3 | D． | 9 |
3．已知函数f（x）=（2+x）2-3x，则f′（1）为（ ）
| A． | 6 | B． | 0 | C． | 3 | D． | 7 |
10．抛物线y2=4x的焦点为F，抛物线上一点M在其准线上的射影为N，若∠NMF=$\frac{2π}{3}$，则M点的横坐标系是（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{2}{3}$ | D． | $\frac{3}{4}$ |
7．已知抛物线C：y2=8x的焦点为F，准线为1，Q是直线l上的一点，P是直线QF与C的一个交点，若$\overrightarrow{QF}$=4$\overrightarrow{PF}$，则△POF（O为坐标原点）的面积为（ ）
| A． | 2 | B． | 2$\sqrt{3}$ | C． | $\sqrt{2}$ | D． | 2$\sqrt{2}$ |
8．已知实数x，y满足$\left\{\begin{array}{l}{2x+y≤2}\\{x≥0}\\{x+y≥0}\end{array}\right.$，z=（x+1）2+（y+2）2，则z的最小值为（ ）
| A． | $\frac{3\sqrt{2}}{2}$ | B． | $\frac{9}{2}$ | C． | $\sqrt{5}$ | D． | 5 |