题目内容
18.已知定义在R上的函数f(x)=x2-cosx,若a=f(30.3),b=f(logπ3),c=f(log3$\frac{1}{9}$),则a,b,c的大小关系是( )| A. | a>b>c | B. | c>b>a | C. | c>a>b | D. | a>c>b |
分析 求出f(x)的导数,得到函数的单调区间,从而比较函数值的大小即可.
解答 解:f(x)=x2-cosx,f′(x)=2x+sinx,f″(x)=2+cosx>0,
∴f′(x)在R递增,而f′(0)=0,
∴x∈(-∞,0)时,f′(x)<0,f(x)递减,
x∈(0,+∞)时,f′(x)>0,f(x)递增,
而f(-x)=x2-cos(-x)=x2-cosx=f(x),
∴f(x)为偶函数,
∵2>30.3>1,0<logπ3<1,log3$\frac{1}{9}$=-2,
∴f(log3$\frac{1}{9}$)=f(-2)=f(2),
∴logπ3<30.3<2,
∴f(logπ3)<f(30.3)<f(log3$\frac{1}{9}$=),
∴c>a>b,
故选:C.
点评 本题考查了函数的单调性问题,考查导数的应用以及函数的奇偶性问题,是一道中档题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
13.在如图所示的计算1+5+9+…+2013的程序框图中,判断框内应填入( )
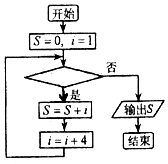

| A. | i≤504 | B. | i≤2009 | C. | i≤2013 | D. | i<2013 |
10.在△ABC中,a,b,c分别为内角A,B,C的对边,且2absinC=$\sqrt{3}$(b2+c2-a2),若a=$\sqrt{13}$,c=3,则△ABC的面积为( )
| A. | 3 | B. | 3$\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | $\frac{3\sqrt{3}}{2}$ |