题目内容
某厂生产化工原料，当年产量在150吨到250吨时，年生产总成本y（万元）与年产量x（吨）之间的关系可近似表示为y=
．
（1）为使每吨平均成本最低，年产量指标应定在多少吨？（注：平均成本=
）
（2）若出厂价为每吨16万元，为获得最大的利润，年产量指标应定在多少吨，并求出最大利润．
解：（1）依题意，每吨平均成本为
（万元），
则
30
30=10
当且仅当
，即x=200时取等号，又150＜200＜250，
所以年产量为200吨时，每吨平均成本最低为10万元．
（2）设年获得的总利润为Q（万元），
则Q=16x
=
=
又150＜230＜250，所以年产量为230吨时，可获最大年利润为1290万吨．
分析：（1）依题意，每吨平均成本为（万元），从而可得函数，再利用基本不等式求解；（2）设年获得的总利润为Q（万元），构建函数，再利用配方法求最值．
点评：本题重在考查函数的构建，考查运用二次函数性质求最值常用配方法或公式法．
（万元），则
30 30=10当且仅当
，即x=200时取等号，又150＜200＜250，所以年产量为200吨时，每吨平均成本最低为10万元．
（2）设年获得的总利润为Q（万元），
则Q=16x
==又150＜230＜250，所以年产量为230吨时，可获最大年利润为1290万吨．分析：（1）依题意，每吨平均成本为
（万元），从而可得函数，再利用基本不等式求解；（2）设年获得的总利润为Q（万元），构建函数，再利用配方法求最值．点评：本题重在考查函数的构建，考查运用二次函数性质求最值常用配方法或公式法．
练习册系列答案
阅读快车系列答案
相关题目
如图，P是双曲线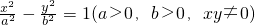
上的动点，F1、F2是双曲线的左右焦点，M是∠F1PF2的平分线上一点，且F2M⊥MP．某同学用以下方法研究|OM|：延长F2M交PF1于点N，可知△PNF2为等腰三角形，且M为F2N的中点，得
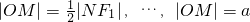．类似地：P是椭圆
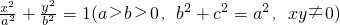上的动点，F1、F2是椭圆的左右焦点，M是∠F1PF2的平分线上一点，且F2M⊥MP，则|OM|的取值范围是________．
与
的夹角为钝角的充要条件是________．
的两条渐近线相交得二交点，若二交点间的距离为4，则该双曲线的离心率为
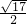
如图所示，Rt△ABC内接于圆，∠ABC=60°，PA是圆的切线，A为切点，PB交AC于E，交圆于D．若PA=AE，PD=
，BD=
，则AP=________，AC=________．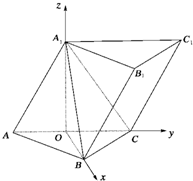
如图，已知三棱柱ABC-A1B1C1的侧棱与底面所成的角为60°，AB=BC，A1A=A1C=2，AB⊥BC，侧面AA1C1C⊥底面ABC．
如图，已知四棱锥P-ABCD中，PA⊥平面CDAB，ABCD是直角梯形，AD∥BC，∠BAD=90°，BC=2，PA=AB=1．求点D到平面PBC的距离．
的定义域．
________．