题目内容
16.在直角坐标系xOy中,圆C的参数方程为$\left\{\begin{array}{l}{x=3+2cosθ}\\{y=-4+2sinθ}\end{array}\right.$(θ为参数).(Ⅰ)以原点为极点、x轴正半轴为极轴建立极坐标系,求圆C的极坐标方程;
(Ⅱ)已知A(-2,0),B(0,2),圆C上任意一点M(x,y),求△ABM面积的最大值并写出此时点M的坐标.
分析 (Ⅰ)利用同角三角函数的关系消元得到圆C的方程,将直线l的参数方程左侧展开,利用极坐标与直角坐标的对应关系得出直线l的直角坐标方程;
(Ⅱ)先求点M(x,y)到直线AB:x-y+2=0的距离为d=$\frac{|2cosθ-2sinθ+9|}{\sqrt{2}}$,再求△ABM的面积S=$\frac{1}{2}×|AB|×d$=|2cos$θ-2sinθ+9|=|2\sqrt{2}$sin$(\frac{π}{4}-θ)$+9|,然后求最值.
解答 解:(1)圆C的参数方程为$\left\{\begin{array}{l}{x=3+2cosθ}\\{y=-4+2sinθ}\end{array}\right.$(θ为参数).
所以普通方程为(x-3)2+(y+4)2=4.
∴圆C的极坐标方程:ρ2-6ρcosθ+8ρsinθ+21=0.
(2)点M(x,y)到直线AB:x-y+2=0的距离为d=$\frac{|2cosθ-2sinθ+9|}{\sqrt{2}}$,
△ABM的面积S=$\frac{1}{2}×|AB|×d$=|2cos$θ-2sinθ+9|=|2\sqrt{2}$sin$(\frac{π}{4}-θ)$+9|
所以△ABM面积的最大值为9+2$\sqrt{2}$,此时点M为(3+$\sqrt{2}$,-4-$\sqrt{2}$).
点评 本题考查了参数方程,极坐标方程与普通方程的转化,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.已知一个几何体的三视图如图所示,若该几何体的体积为$\frac{10}{3}$,则a+b2的最小值为( )
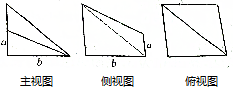

| A. | 4$\sqrt{3}$ | B. | 3$\sqrt{3}$ | C. | 4 | D. | 4$\sqrt{2}$ |
7.清华大学自主招生考试题中要求考生从A,B,C三道题中任选一题作答,考试结束后,统计数据显示共有600名学生参加测试,选择A,B,C三题答卷数如下表:
(Ⅰ)负责招生的教授为了解参加测试的学生答卷情况,现用分层抽样的方法从600份答案中抽出若干份答卷,其中从选择A题作答的答卷中抽出了3份,则应分别从选择B,C题作答的答卷中各抽出多少份?
(Ⅱ)测试后的统计数据显示,A题的答卷得优的有60份,若以频率作为概率,在(Ⅰ)问中被抽出的选择A题作答的答卷中,记其中得优的份数为X,求X的分布列及其数学期望E(X).
| 题 | A | B | C |
| 答卷数 | 180 | 300 | 120 |
(Ⅱ)测试后的统计数据显示,A题的答卷得优的有60份,若以频率作为概率,在(Ⅰ)问中被抽出的选择A题作答的答卷中,记其中得优的份数为X,求X的分布列及其数学期望E(X).
 如图,在五棱锥P-ABCDE中,PA⊥平面ABCDE,AB∥CD,AC∥ED,AE∥BC,∠ABC=45°,AB=2$\sqrt{2}$,BC=2AE=4,三角形PAB是等腰三角形.
如图,在五棱锥P-ABCDE中,PA⊥平面ABCDE,AB∥CD,AC∥ED,AE∥BC,∠ABC=45°,AB=2$\sqrt{2}$,BC=2AE=4,三角形PAB是等腰三角形.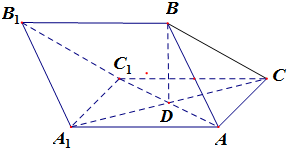 在三棱柱ABC-A1B1C1中,AB=AC=AA1=BC1=2,∠AA1C1=60°,BC=$\sqrt{6}$,AC1与A1C相交于点D.
在三棱柱ABC-A1B1C1中,AB=AC=AA1=BC1=2,∠AA1C1=60°,BC=$\sqrt{6}$,AC1与A1C相交于点D.