题目内容
4.已知平面向量$\overrightarrow a,\overrightarrow b$满足$|{\overrightarrow a}$$|=1,\overrightarrow a$与$\overrightarrow b-\overrightarrow a$的夹角为60°,记$\overrightarrow m=λ\overrightarrow a+({1-λ})\overrightarrow b({λ∈R})$,则$|{\overrightarrow m}$|的取值范围为[$\frac{\sqrt{3}}{2}$,+∞).分析 由共线原理可知三向量的终点共线,作出图形,求出最短距离即可得出答案.
解答 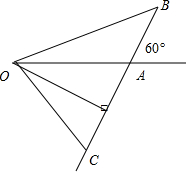 解:设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{m}$,
解:设$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,$\overrightarrow{OC}$=$\overrightarrow{m}$,
则OA=1,∠OAB=120°,
∵$\overrightarrow m=λ\overrightarrow a+({1-λ})\overrightarrow b({λ∈R})$,
∴A,B,C三点共线,
O到直线AB的距离d=OA•sin60°=$\frac{\sqrt{3}}{2}$,
∴OC≥$\frac{\sqrt{3}}{2}$,
故答案为:[$\frac{\sqrt{3}}{2}$,+∞).
点评 本题考查了平面向量的基本定理,属于中档题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
14.直线m:kx+y+4=0(k∈R) 是圆C:x2+y2+4x-4y+6=0的一条对称轴,过点A(0,k)作斜率为1的直线n,则直线n被圆C所截得的弦长为( )
| A. | $\sqrt{14}$ | B. | $\sqrt{2}$ | C. | $\sqrt{6}$ | D. | 2$\sqrt{6}$ |
9.下列说法正确的是( )
| A. | 命题“?x0∈R,2${\;}^{{x}_{0}}$>1”的否定是“?x∈R,2x≤1” | |
| B. | 命题“若x=y,则x2=y2”的否命题是“若x=y,则x2≠y2” | |
| C. | p:?x∈R,x2+1≥1,q:在△ABC中,若sinA=$\frac{1}{2}$,则A=$\frac{π}{6}$,则p∧q为真命题 | |
| D. | 若平面α⊥平面β,直线a?α,直线b?β,则a⊥b |
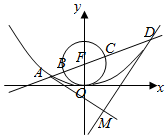 已知抛物线x2=2py(p>0)的焦点为F,直线x=4与x轴的交点为P,与抛物线的交点为Q,且$|{QF}|=\frac{5}{4}|{PQ}|$.
已知抛物线x2=2py(p>0)的焦点为F,直线x=4与x轴的交点为P,与抛物线的交点为Q,且$|{QF}|=\frac{5}{4}|{PQ}|$.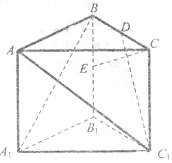 在棱长为2的正三棱柱ABC-A1B1C1中,D,E分别是BC,BB1的中点.
在棱长为2的正三棱柱ABC-A1B1C1中,D,E分别是BC,BB1的中点. ,则
,则
 C.1 D.
C.1 D.