题目内容
(本小题满分12分)在平行六面体 中,
中,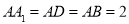 ,
,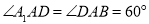 ,
, 是
是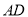 的中点.
的中点.

(1)证明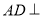 面
面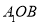 ;
;
(2)当平面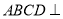 平面
平面 ,求
,求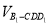 .
.
(1)证明见解析;(2)1.
【解析】
试题分析:(1)本题证明线面垂直,根据纯平面垂直的判定定理,只要证明直线 与平面
与平面 内的两条相交直线垂直即可,而从已知条件可看出只要在
内的两条相交直线垂直即可,而从已知条件可看出只要在 和
和 中利用正弦定理及勾股定理就能证得
中利用正弦定理及勾股定理就能证得 ,
, ;(2)本题要求三棱锥的体积,而这个三棱锥的顶点都是平行六面体
;(2)本题要求三棱锥的体积,而这个三棱锥的顶点都是平行六面体 的顶点,因此我们利用棱锥的体积公式进行转化,
的顶点,因此我们利用棱锥的体积公式进行转化,
 ,而对这个平行六面体来讲,由于有平面
,而对这个平行六面体来讲,由于有平面 平面
平面 ,
, ,因此就有
,因此就有 平面
平面 ,
, 就是高,体积易求得.
就是高,体积易求得.
试题解析:(1)证明:取 的中点
的中点 ,连接
,连接
由 同理
同理
 平面
平面 ,
,
(2) 平面
平面

由(1) 又平面
又平面
 平面
平面

 平面
平面




考点:(1)直线与平面垂直;(2)棱锥的体积.

练习册系列答案
 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
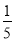 和
和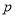 ,若在任意时刻至多有一个系统发生故障的概率为
,若在任意时刻至多有一个系统发生故障的概率为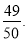
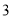 次相互独立的检测中不发生故障的次数为随机变量
次相互独立的检测中不发生故障的次数为随机变量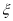 ,求
,求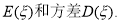
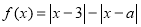 .
.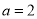 时,解不等式
时,解不等式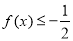 ;
;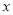 ,使得不等式
,使得不等式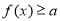 成立,求实数
成立,求实数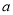 的取值范围.
的取值范围.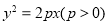 ,过抛物线上一点
,过抛物线上一点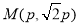 和抛物线的焦点
和抛物线的焦点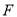 作直线
作直线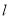 交抛物线于另一点
交抛物线于另一点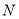 ,则
,则 ( )
( )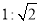 B.
B.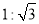 C.
C.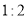 D.
D.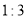
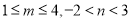 ,求
,求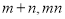 的取值范围;
的取值范围;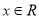 ,
,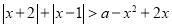 恒成立,求
恒成立,求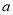 的取值范围.
的取值范围. ,
, ,满足
,满足 ,则
,则 .
.
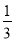 B.
B.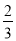 C.
C.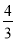 D.
D.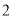
 满足
满足 ,且
,且 ,则
,则 与
与 的夹角为 .
的夹角为 .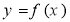 在定义域内给定区间[a,b]上存在
在定义域内给定区间[a,b]上存在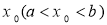 ,满足
,满足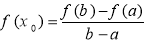 ,则称函数
,则称函数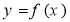 是[a,b]上的“平均值函数”,
是[a,b]上的“平均值函数”, 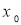 是它的一个均值点.例如
是它的一个均值点.例如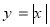 是[-2,2]上的“平均值函数”,O就是它的均值点.若函数
是[-2,2]上的“平均值函数”,O就是它的均值点.若函数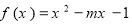 是[-1,1]上的“平均值函数”,则实数
是[-1,1]上的“平均值函数”,则实数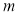 的取值范围是 .
的取值范围是 .