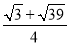题目内容
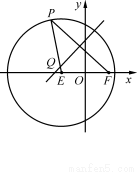
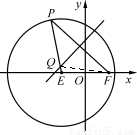
(本小题满分13分)如图,已知圆E: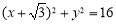 ,点
,点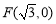 ,P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.
,P是圆E上任意一点.线段PF的垂直平分线和半径PE相交于Q.
(Ⅰ)求动点Q的轨迹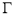 的方程;
的方程;
(Ⅱ)设直线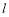 与(Ⅰ)中轨迹
与(Ⅰ)中轨迹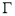 相交于
相交于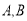 两点,直线
两点,直线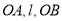 的斜率分别为
的斜率分别为 (其中
(其中
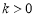 ).△
).△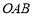 的面积为
的面积为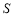 , 以
, 以 为直径的圆的面积分别为
为直径的圆的面积分别为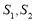 .若
.若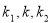 恰好构成等比数列, 求
恰好构成等比数列, 求
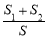 的取值范围.
的取值范围.
(Ⅰ)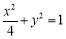 ;(Ⅱ)
;(Ⅱ)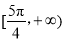
【解析】
试题分析: (Ⅰ)由椭圆的定义结合题意分析可知动点Q的轨迹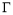 是以E,F为焦点,长轴长为4的椭圆,即可列出其轨迹方程;(Ⅱ)设直线
是以E,F为焦点,长轴长为4的椭圆,即可列出其轨迹方程;(Ⅱ)设直线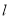 的方程为
的方程为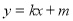 ,
,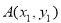 ,
,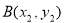 ,
,
联立直线方程和椭圆方程,整理得到关于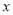 的方程,根据韦达定理求出
的方程,根据韦达定理求出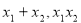 ,借助于
,借助于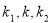 构成等比数列,即
构成等比数列,即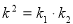 ,解出
,解出 ,由弦长公式和点到直线距离公式分别确定
,由弦长公式和点到直线距离公式分别确定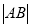 和
和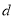 ,进而求出
,进而求出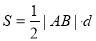
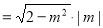 ,由圆的面积公式求出
,由圆的面积公式求出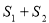
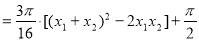
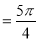 为定值,由不等式的性质,
为定值,由不等式的性质,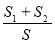
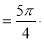
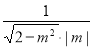
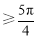 (当且仅当
(当且仅当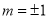 时等号成立)即可求出.
时等号成立)即可求出.
试题解析:
(Ⅰ)连结QF,根据题意,|QP|=|QF|,则|QE|+|QF|=|QE|+|QP|=4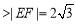 ,故动点Q的轨迹
,故动点Q的轨迹 是以E,F为焦点,长轴长为4的椭圆. 2分
是以E,F为焦点,长轴长为4的椭圆. 2分
设其方程为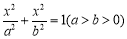 ,
,
可知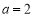 ,
,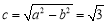 ,则
,则 , 3分
, 3分
所以点Q的轨迹 的方程为
的方程为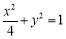 . 4分
. 4分
(Ⅱ)设直线 的方程为
的方程为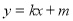 ,
,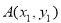 ,
,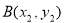
由 可得
可得 ,
,
由韦达定理有: 且
且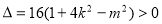 6分
6分
∵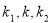 构成等比数列,
构成等比数列,
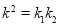 =
=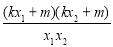 ,即:
,即: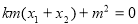
由韦达定理代入化简得: .∵
.∵ 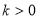 ,
,
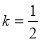 . 8分
. 8分
此时 ,即
,即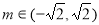 .
.
又由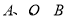 三点不共线得
三点不共线得 ,从而
,从而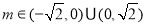 .
.
故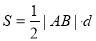
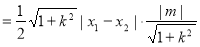
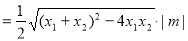
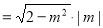 10分
10分
∵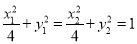
则 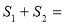
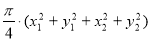
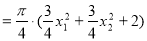
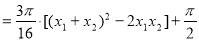
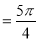 为定值. 12分
为定值. 12分
∴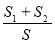
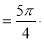
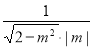
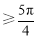
∴当且仅当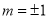 时等号成立.
时等号成立.
综上: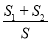 的取值范围是
的取值范围是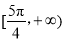 . 13分
. 13分
考点:1、椭圆的定义;2、弦长公式;3、最值问题.

 阅读快车系列答案
阅读快车系列答案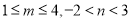 ,求
,求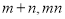 的取值范围;
的取值范围;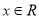 ,
,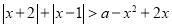 恒成立,求
恒成立,求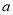 的取值范围.
的取值范围.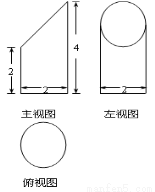
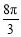 B.
B.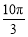 C.
C.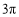 D.
D.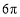
 ,
, ,则集合
,则集合 = .
= .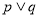 为真命题”是“
为真命题”是“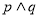 为真命题”的( ).
为真命题”的( ).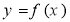 在定义域内给定区间[a,b]上存在
在定义域内给定区间[a,b]上存在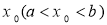 ,满足
,满足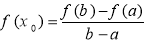 ,则称函数
,则称函数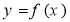 是[a,b]上的“平均值函数”,
是[a,b]上的“平均值函数”, 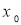 是它的一个均值点.例如
是它的一个均值点.例如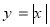 是[-2,2]上的“平均值函数”,O就是它的均值点.若函数
是[-2,2]上的“平均值函数”,O就是它的均值点.若函数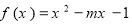 是[-1,1]上的“平均值函数”,则实数
是[-1,1]上的“平均值函数”,则实数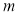 的取值范围是 .
的取值范围是 .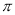 ,—1),C(
,—1),C(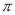 ,1),D(0,1),正弦曲线
,1),D(0,1),正弦曲线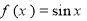 和余弦曲线
和余弦曲线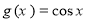 在矩形ABCD内交于点F,向矩形ABCD区域内随机投掷一点,则该点落在阴影区域内的概率是( ).
在矩形ABCD内交于点F,向矩形ABCD区域内随机投掷一点,则该点落在阴影区域内的概率是( ).
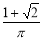 B.
B.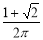 C.
C.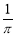 D.
D.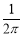
 中,
中, ,
, ,
, ,则
,则 边上的高为( )
边上的高为( ) B.
B.
 D.
D.
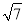 ,BC=2,B=60°,则BC边上的高等于( )
,BC=2,B=60°,则BC边上的高等于( )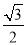 B.
B.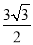 C.
C.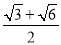 D.
D.