题目内容
已知集合A={x|x2-1=0},集合B={x|(k+1)x2+(k+2)x+2=0},若集合A与集合B有元素相同,则实数k的取值的集合的子集的个数为( )
| A、2 | B、4 | C、8 | D、16 |
考点:子集与真子集
专题:集合
分析:先求出结合A的元素,通过讨论集合B中所含的元素,从而得到k的取值的个数,进而得到答案.
解答:
解:集合A={1,-1}有2个元素,
若集合B有1这个元素,
得到2k+5=0,k=-
,
若集合B有-1这个元素,将x=-1代入,不合题意,
∴实数k的取值有1个,
满足条件的集合的子集的个数为2个,
故选:A.
若集合B有1这个元素,
得到2k+5=0,k=-
| 5 |
| 2 |
若集合B有-1这个元素,将x=-1代入,不合题意,
∴实数k的取值有1个,
满足条件的集合的子集的个数为2个,
故选:A.
点评:本题考查了方程问题,集合的概念问题,是一道基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若二项式(x2-
)n的展开式中,含x14的项是第3项,则n=( )
| 1 |
| x |
| A、8 | B、9 | C、10 | D、11 |
下列函数中,为奇函数的是( )
| A、f(x)=x-1 |
| B、f(x)=x |
| C、f(x)=-3x+2 |
| D、f(x)=2x2 |
关于x的不等式x2-4x-5>0的解集是 ( )
| A、{x|x<-1或x>5} |
| B、{x|x<1或x>5} |
| C、{x|-1<x<5} |
| D、{x|1<x<5} |
设a=log20.3,b=20.3,c=0.32,则下列不等式成立的是( )
| A、c<b<a |
| B、b<a<c |
| C、a<c<b |
| D、c<a<b |
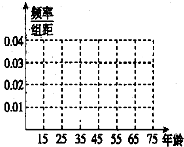 2014年我国公布了新的高考改革方案,在招生录取制度改革方面,普通高校逐步推行基于统一高考和高中学业水平考试成绩的综合评价、多元录取机制,普通高校招生录取将参考考生的高中学业水平考试成绩和职业倾向性测试成绩.为了解公众对“改革方案”的态度,随机抽查了50人,将调查情况进行整理后制成下表:
2014年我国公布了新的高考改革方案,在招生录取制度改革方面,普通高校逐步推行基于统一高考和高中学业水平考试成绩的综合评价、多元录取机制,普通高校招生录取将参考考生的高中学业水平考试成绩和职业倾向性测试成绩.为了解公众对“改革方案”的态度,随机抽查了50人,将调查情况进行整理后制成下表: