题目内容
1.已知在等比数列{an}中,公比q≠1,a1,a3,a5是等差数列{bn}中的b2,b4,b12,则q=±2.分析 由题意可得:${a}_{3}^{2}={a}_{1}{a}_{5}$,$({b}_{1}+3d)^{2}$=(b1+d)(b1+11d),化简代入q2=$\frac{{a}_{3}}{{a}_{1}}$,即可得出.
解答 解:∵在等比数列{an}中,公比q≠1,a1,a3,a5是等差数列{bn}中的b2,b4,b12,
设等差数列{bn}的公差为d,
∴${a}_{3}^{2}={a}_{1}{a}_{5}$,$({b}_{1}+3d)^{2}$=(b1+d)(b1+11d),化为:d=-3b1.
∴q2=$\frac{{a}_{3}}{{a}_{1}}$=$\frac{{b}_{1}+3d}{{b}_{1}+d}$=$\frac{-8{b}_{1}}{-2{b}_{1}}$=4,
∴q=±2.
故答案为:±2.
点评 本题考查了等差数列与等比数列的通项公式及其性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.如果函数f(x)=x2-ax-3在区间(-∞,3]上单调递减,则实数a满足的条件使( )
| A. | a≤6 | B. | a≥6 | C. | a≥3 | D. | a≥-3 |
9.圆x2+y2+Dx+Ey-4=0的圆心为(-1,2),则圆的半径为( )
| A. | 6 | B. | 9 | C. | 3 | D. | 2 |
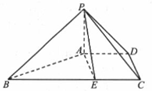 如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为梯形,AD∥BC,BC=6,PA=AD=CD=2,E为BC上一点且BE=$\frac{2}{3}$BC,PB⊥AE.
如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为梯形,AD∥BC,BC=6,PA=AD=CD=2,E为BC上一点且BE=$\frac{2}{3}$BC,PB⊥AE.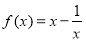 .
.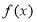 在区间
在区间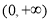 上为增函数;
上为增函数;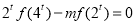 ,当
,当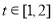 时,求实数
时,求实数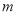 的取值范围.
的取值范围. 为常数,函数
为常数,函数 在
在 内有两个极值点,则实数
内有两个极值点,则实数 的取值范围为( )
的取值范围为( ) B.
B.
 D.
D.
 在
在 上单调递减,则实数
上单调递减,则实数 的取值范围是 .
的取值范围是 .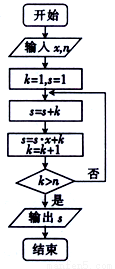
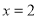 ,
,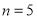 ,求输出的
,求输出的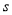 的值;
的值;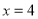 ,输出的
,输出的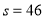 ,求输入的
,求输入的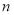 (
(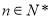 )的值.
)的值.